Feladat:	1183. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: -
Megoldó(k):	Frey Julianna ,  Hosszú Ferenc ,  Selényi Péter
Füzet:	1968/október, 73 - 75. oldal		PDF  |  MathML
Témakör(ök):	Síkidomok átdarabolása, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/február: 1183. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.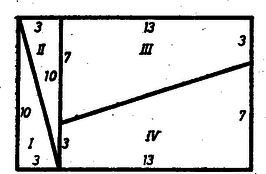 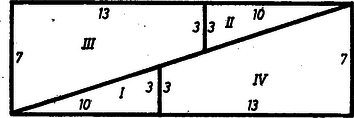    1. ábra   I. A meglepő eredmény magyarázata az, hogy a $23\times 7$ cm méretű téglalapnak a berajzolt átló mentén egy hosszú, lapos, paralelogramma alakú része nincs lefedve. Ha az I. derékszögű háromszög átfogója rajta lenne az átlón, akkor I. hasonló lenne a téglalap feléhez, és a megfelelő befogók aránya egyenlő lenne. Ámde $3:10=0\mathrm{,}3$ és $7:23=0\mathrm{,}3043$, nagyobb amannál, így I. felső csúcsa alatta van az átlónak, s ugyanígy az átló a II. háromszög alsó csúcsának alatta halad el. A második arányból azt is látjuk, hogy I-nek 3 cm-es befogóját az átlóig $0\mathrm{,}043$ cm-rel, azaz nem egészen $0\mathrm{,}5$ mm-rel kellene meghosszabbítani, s ez az ábra kb. $0\mathrm{,}3$-szeres kicsinyítésében kisebb $0\mathrm{,}15$ mm-nél, az ábra vonalvastagságánál. Emiatt nem vesszük észre a hézagot. Ha azonban a $16\times 10$ cm méretű téglalap részeit egy négyzethálós papírlapon kijelölt $23\times 7$ cm méretű téglalapba másoljuk át, a hézag már jól látható. A paralelogramma területe az új és eredeti téglalap területének különbsége, 1 ${\text{cm}}^2$. Mivel a trapézok ferde szára $\sqrt[]{185}\approx 13\mathrm{,}6$ cm, a paralelogrammának erre merőleges magassága, III. és IV. egymáshoz közel haladó oldalainak távolsága, majdnem $3/4$ mm. II. Hasonlóan tetszés szerinti, $a$ és $b$ oldalakkal bíró ($a<b$, természetes számok) téglalapot egyik átlójával együtt négyzethálós papíron megrajzolva kereshetünk az átlóhoz közel álló belső hálózati pontot ‐ ún. rácspontot ‐, mely a közbülső, elhanyagolandó paralelogramma csúcsa lehet, ezt a téglalap középpontjára tükrözve kapjuk a negyedik csúcsot. 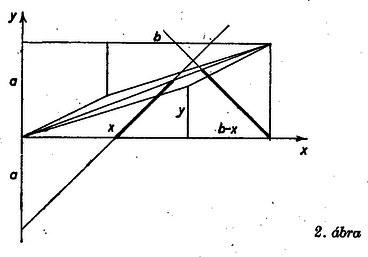    Legyenek a keletkezett két derékszögű háromszög befogói a 2. ábra szerint $x$ és $y$ (természetes számok), ezekből egy $x$, $y$ oldalú téglalapot állíthatunk össze, a két trapézból pedig ‐ ferde száraik menti összeillesztéssel ‐ olyan téglalapot kapunk, melynek oldalai $a+y$ és $b-x$. E két idom egy téglalappá illeszthető össze, ha egy‐egy oldaluk egyenlő, azaz teljesül a következő feltételek valamelyike: ${\displaystyle \begin{array}{c}\hfill {\displaystyle \alpha )x=a+y\mathrm{,}\gamma )x=b-x\mathrm{,}}\hfill \\ \hfill {\displaystyle \beta )y=b-x\mathrm{,}\delta )y=a+y\mathrm{.}}\hfill \end{array}}$ A $\delta$ illesztésmód lehetetlen, a $\gamma$ mód számunkra érdektelen, mert $x=b/2$, csak páros $b$ esetén egész, és ezen a rácsegyenesen a középső paralelogramma átlója a párossága szerint 1 vagy 2 egység, a terület mindenképpen nagy, így csak az első két illesztésmóddal érdemes foglalkoznunk. A $\beta$ módot kielégítő rácspontok csak a téglalap jobb alsó csúcsából kiinduló szögfelezőn kereshetők, az $\alpha$ módra alkalmasak pedig az ábra $y=x-a$ egyenesének vastagon rajzolt szakaszán. Végső soron csak olyan $x$, $y$ számpár ad Zsiga kérdésére megoldást, amellyel a paralelogramma területe 1.   III. Az előírt első számpéldában, egy 260, ill. 261 egységnyi területű téglalap‐pár keresésében $261=3^2\cdot 29$, így csak $9\times 29$, $3\times 87$ és $1\times 261$ méretű téglalapokkal próbálkozhatunk. Mindjárt az elsőben, $a=9$, $b=29$ esetén megfelel az $\alpha$ illesztésmód szerint $x=13$, $y=4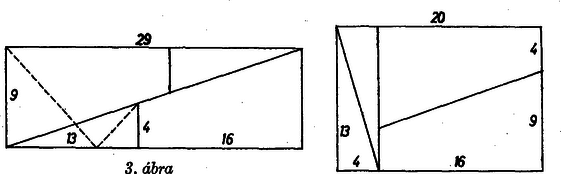$ (3. ábra).     3. ábra   Hasonlóan a 272, 273 számpárhoz a $273=13\cdot 21$ felbontásból, $a=13$, $b=21$ esetén a $\beta$ mód szerint $x=13$, $y=8$ (4. ábra, itt a trapézok fordultak el derékszöggel). 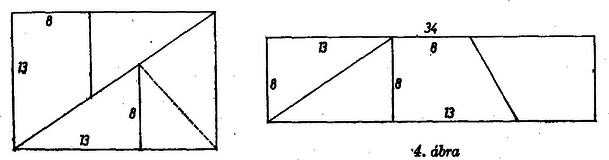    Hasonló próbát bármely szomszédos egész számpárral tehetünk, de eleve nem ígér sikert, ha egyikük prímszám. $a=4$, $b=13$ esetén $x=10$, $y=3$ olyan példára vezet: $a\text{'}=3$, $b=17$, amelyben a területek 52 és 51, a nagyobbik a páros; látjuk a fentiekből, hogy ez nem lényeges különbség.    Frey Julianna (Budapest, Kölcsey F. Gimn., I. o. t.)  Hosszu Ferenc (Budapest, Berzsenyi D. Gimn., I. o. t.)  Selényi Péter (Budapest, Kvassay J. Techn., I. o. t.)  dolgozataiból, több kiegészítéssel, egyszerűsítéssel