Kezdőlap


Feladat:	1180. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Akar László , Kovács Miklós , Martoni Viktor
Füzet:	1969/január, 18 - 20. oldal		PDF \| MathML
Témakör(ök):	Egyenletek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/február: 1180. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A bizonyítandó (3) egyenlőség bal oldalán $n$ azonos felépítésű tag (szorzat) áll; $n = 1$ esetén a bal oldal egyetlen tagja azonos a jobb oldallal.
$n > 1$ esetén a föltevés szerint

\begin{matrix} y_{0} + y_{1} = p (x_{0} + x_{1}) + 2 q, \end{matrix}

így (3) bal oldalának első tagja

\begin{matrix} t_{1} = p (x_{1}^{2} - x_{0}^{2}) + 2 q (x_{1} - x_{0}); \end{matrix}

ugyanígy a második tag, majd az első két tag

s_{2}

összege

\begin{matrix} t_{2} = p (x_{2}^{2} - x_{1}^{2}) + 2 q (x_{2} - x_{1}), \\ s_{2} = t_{1} + t_{2} = p (x_{2}^{2} - x_{0}^{2}) + 2 q (x_{2} - x_{0}), \end{matrix}

és itt a változók 1-es indexű értékei nem szerepelnek, az összegben kiestek.
Ugyanígy az első 3, az első 4,

...

tag összegét felírva, benne az

x_{0}

y_{0}

értékpáron kívül csak egyféle index, az

x_{3}

y_{3}

, ill.

x_{4}

y_{4}

...

értékpár lép fel, a közbülső indexű értékek kiesnek. Ebből sejtjük, hogy az első

i

tag összege bármely

i (> 0)

esetén ilyen alakú:

\begin{matrix} s_{i} = p (x_{i}^{2} - x_{0}^{2}) + 2 q (x_{i} - x_{0}) . \end{matrix}

(4)

Valóban, az

i + 1

-edik tag

\begin{matrix} t_{i + 1} = (y_{i} + y_{i + 1}) (x_{i + 1} - x_{i}) = p (x_{i + 1}^{2} - x_{i}^{2}) + 2 q (x_{i + 1} - x_{i}), \end{matrix}

és így az első

i + 1

tag összege

\begin{matrix} s_{i + 1} = s_{i} + t_{i + 1} = p (x_{i + 1}^{2} - x_{0}^{2}) + 2 q (x_{i + 1} + x_{0}), \end{matrix}

ami azonos (4)-gyel, ha az

i

indexeket

i + 1

-gyel pótoljuk. Ezzel bebizonyítottuk, hogy (4) helyes.
Ezt

i = n

esetére alkalmazva (3) bal oldala, kellő további alakítással

\begin{matrix} s_{n} = p (x_{n}^{2} - x_{0}^{2}) + 2 q (x_{n} - x_{0}) = (p x_{n} + p x_{0}) (x_{n} - x_{0}) + 2 q (x_{n} - x_{0}) = \\ [(p x_{n} + q) + (p x_{0} + q)] (x_{n} - x_{0}) = (y_{n} + y_{0}) (x_{n} - x_{0}), \end{matrix}

azonos a jobb oldallal. Eszerint az állítás helyes.
A bizonyításban nem volt szükség az (1) egyenlőtlenségre, tehát az állítás anélkül is érvényes (az

y = p x + q

függvény minden

x

-re értelmezve van).
Számításunk

p = 0

esetén is érvényes, ebben az esetben azonban közvetlenül könnyebben belátható. Ekkor

y_{0} = y_{1} = ... = y_{n} = q

, a (3)-beli szorzatok első tényezője

2 q

, közös.

Martoni Viktor (Veszprém, Lovassy L. Gimn., I. o. t.)
Akar László (Budapest, Fazekas M. Gyak. Gimn., I. o. t.)

II. megoldás.

α

) Egyszerű geometriai jelentést tulajdoníthatunk (3)-nak, ha a (2) értékek egyike sem negatív, ebben (1)-et is felhasználjuk.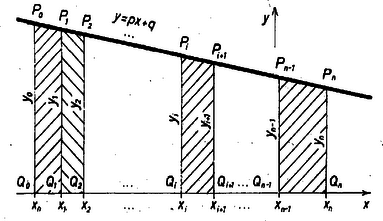

(1) és (2) összetartozó értékpárjai a derékszögű koordináta-rendszerben az

y = p x + q

függvény képén, ami egyenes vonal,

n + 1

pontot jelölnek ki, legyenek ezek rendre

P_{0}

P_{1}

...

P_{n}

, és legyen az

x

tengelyen levő vetületük rendre

Q_{0}

Q_{1}

Q_{2}

...

Q_{n}

. Két-két szomszédos pontpár:

P_{i}

Q_{i}

. és

P_{i + 1}

Q_{i + 1}

, ahol

i = = 0, 1, 2, ..., n - 1

, egy derékszögű trapéz négy csúcsa, hiszen

P_{i} Q_{i} ∣_{i + 1} Q_{i + 1} ⊥ Q_{i} Q_{i + 1}

, a trapéz párhuzamos oldalainak hossza

P_{i} Q_{i} = y_{i}

P_{i + 1} Q_{i + 1} = y_{i + 1}

, magassága pedig

Q_{i} Q_{i + 1} = x_{i + 1} - x_{i}

(

> 0

). Másrészt a

P_{0} Q_{0} Q_{n} P_{n} = T

négyszög is derékszögű trapéz, ennek párhuzamos oldalai

y_{0}

és

y_{n}

, magassága

x_{n} - x_{0}

. Ha

y_{0} = 0

,vagy

y_{n} = 0

, akkor

Q_{0}

azonos

P_{0}

-lal, ill.

Q_{n}

azonos

P_{n}

-nel, a trapézsorozat elején vagy a végén egy derékszögű háromszög áll, és ekkor

T

is elfajul a

P_{0} Q_{n} P_{n}

, ill.

P_{0} Q_{0} P_{n}

derékszögű háromszöggé. Ha pedig

p = 0

és

q > 0

, akkor speciálisan téglalapokat határoznak meg a mondott pontpárok és a

P_{0}

Q_{0}

és

P_{n}

Q_{n}

párok is.
Mármost (3) jobb oldala a

T

trapéz területének 2-szeresét jelenti, a bal pedig annak az

n

trapéznak a 2-szereséből képezett összeg, amelyre

T

-t az alapjaival párhuzamos

P_{1} Q_{1}

P_{2} Q_{2}

...

P_{n - 1} Q_{n - 1}

szakaszok felosztják, így (3) helyessége nyilvánvaló.

β

) Ha a (2) számok között negatív is van, jelölje közülük a legkisebbiket

y^{*}

. Így az

\begin{matrix} y_{i}^{*} = y_{i} - y^{*} \end{matrix}

számok nem negatívok, és az

y = p x + q - y^{*}

függvény megfelelő helyen felvett értékeivel egyenlők, tehát az

α

) rész szerint érvényes rájuk, hogy

\begin{matrix} (y_{0}^{*} + y_{1}^{*}) (x_{1} - x_{0}) + ... + (y_{n - 1}^{*} + y_{n}^{*}) (x_{n} - x_{n - 1}) = (y_{0}^{*} + y_{n}^{*}) (x_{n} - x_{0}) \end{matrix}

(3*)

Mármost (3*) bal oldala a

\begin{matrix} - 2 y^{*} (x_{1} - x_{0}) - ... - 2 y^{*} (x_{n} - x_{n - 1}) = - 2 y^{*} (x_{n} - x_{0}) \end{matrix}

értékkel nagyobb (3) bal oldalánál, és ugyanennyivel nagyobb (3*) jobb oldala is (3) jobb oldalánál, tehát (3) is igaz. (A "nagyobb'' állításnál természetesen figyelembe veendő, hogy

y^{*} < 0

Kovács Miklós (Miskolc, Földes F. Gimn., II. o. t.)