Feladat:	1177. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1980/április, 159 - 161. oldal		PDF  |  MathML
Témakör(ök):	Forgatva nyújtás, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/január: 1177. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.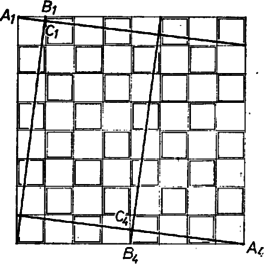   1. ábra   1. Először megmutatjuk, hogy minden forgatva nyújtásnál az elfordítás és a nyújtás sorrendje felcserélhető. Legyen az elfordítandó háromszög $ABC$, a forgatva nyújtás középpontja $K$, szöge $\phi$, aránya $\lambda$ (2. ábra). Ha először az $ABC=H$ háromszöget $\phi$ szöggel elforgatjuk, kapjuk $H_1$-et, majd ezt $\lambda$ arányban nagyítva kapjuk $H_2$-t. Ha most $H_1$-et és $H_2$-t együtt visszaforgatjuk $\phi$ szöggel, $H_1$ $H$-ba, $H_2$ pedig valamilyen $H_3$-ba kerül. Mivel a forgatás aránytartó, ezért $H$-t $K$-ból $\lambda$ arányban kinagyítva $H_3$-t fogjuk kapni. $H_3$-t pedig $\phi$ szöggel elforgatva $H_2$-be jutunk, ugyanoda, mint az előbb. 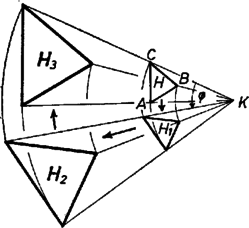  2. ábra   2. Most felhasználjuk, hogy az $A_1{A}_4$, $B_1{B}_4$ és $C_1{C}_4$ egyenesek egy ponton mennek keresztül. Legyen ez a pont $K$ (3. ábra). $K$ körül az $A_1{B}_1{C}_1=H_1$ háromszöget ${180}^{\circ }$-kal elforgatva kerüljön a $H_3$ helyzetbe. Mivel a két eredeti ($H_1$ és $H_4$) háromszögben a megfelelő oldalak párhuzamosak, azért így lesz ez a $H_3$ és $H_4$ háromszögek esetében is, vagyis a két háromszög hasonló lesz. Másrészt a megfelelő csúcsokat összekötő egyenesek egymást $K$-ban metszik, azért $K$-ból a $H_3$ háromszöget megfelelő arányban kinagyítva éppen $H_4$-be jutunk. Ez az arány megegyezik a két háromszög hasonlósági arányával, vagyis 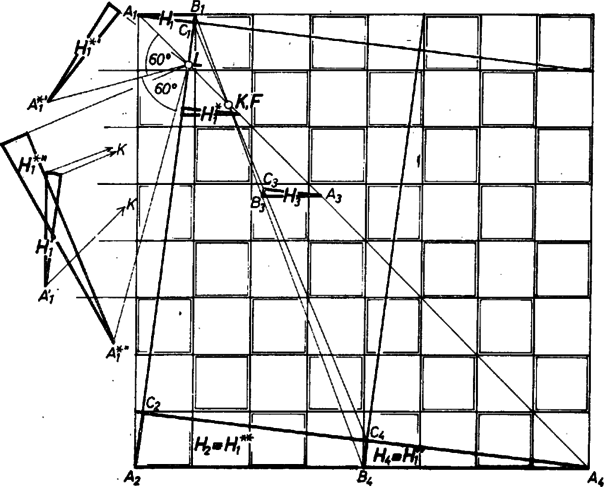$1:4$-gyel.   3. ábra   3. A 2.-ben leírt forgatva nyújtást a következőképpen bontjuk két részre: a) $K$ körül $H_1$-t $\phi ={90}^{\circ }$-kal forgatjuk el, az arányossági tényező $\lambda =2$. Így $H{\text{'}}_1$-t kapjuk. Ezt tovább forgatjuk ${90}^{\circ }$-kal, majd ezt is $\lambda =2$ arányban nagyítjuk $K$-ból. Így eljutunk $H\text{'}{\text{'}}_1$-höz. Ez azonos lesz $H_4$-gyel, ugyanis $H_4$-et összesen ${90}^{\circ }+{90}^{\circ }={180}^{\circ }$-kal forgattuk el, és $2\cdot 2=4$-szeresére nyújtottuk. $H{\text{'}}_1$ nyilván megszerkeszthető, ${90}^{\circ }$-kal elforgatni és kétszeresére nyújtani könnyen lehet. Már csak az van hátra, hogy megmutassuk, az $A_1{A}_4$, $B_1{B}_4$ és $C_1{C}_4$ egyenesek egy ponton mennek át. Ehhez nyilván elegendő azt megmutatnunk, hogy $B_1{B}_4$ és $C_1{C}_4$ metszéspontja egyforma messze van a sakktábla széleitől. Legyen e két egyenes metszéspontja $F$. Az $F{B}_1{C}_1$ és $F{B}_4{C}_4$ háromszögek hasonlók, mivel oldalaik párhuzamosak. Hasonlóságuk aránya $1:4$, mert e két háromszög hasonlóságának aránya megegyezik a $H_1$ és $H_4$ háromszögek hasonlóságának arányával, hiszen egy‐egy közös oldaluk van. Így a metszéspont $B_1{B}_4$-et $1:4$ arányban osztja, tehát távolsága $A_1{B}_1$-től 8/5, $A_1{A}_2$-től $1+3/5=8/5$, e két távolság valóban egyenlő. 4. Állítjuk, hogy olyan hasonló háromszögpár, melyet egymásba átvivő forgatva nyújtás felbontható 3 kívánt forgatva nyújtásba, az $A_1{B}_1{C}_1=H_1$, valamint az $A_2{A}_4{C}_2=H_2$ háromszögek. Legyen ugyanis $A_1{A}_4$ és $B_1{A}_2$ metszéspontja $L$. $L$ körül ${180}^{\circ }$-kal elforgatva $H_1$-et $H_1^{*}$-ba jutunk Mivel $H_1$ és $H_2$ hasonlók voltak, hiszen megfelelő oldalaik párhuzamosak, $H_1^{*}$ és $H_2$ is hasonlók lesznek, hasonlóságuk aránya $A_1{B}_1:A_2{A}_4=1:8$, mivel itt a megfelelő csúcsokat összekötő egyenesek egy ponton mennek keresztül, $L$-ből történő $\lambda =1:8$ arányú nagyítás $H_1^{*}$-t éppen $H_2$-be viszi. Ezt az elforgatást a következő háromra lehet felbontani: $H_1$-et $L$ körül $\phi ={60}^{\circ }$-kal elforgatjuk, majd $\lambda =2$ arányban nagyítjuk. Ezt még kétszer megismételve kapjuk $H_1^{**}$-ot. Ez megegyezik $H_2$-vel, hiszen összesen ${60}^{\circ }+{60}^{\circ }+{60}^{\circ }={180}^{\circ }$-kal forgattunk el és $2\cdot 2\cdot 2=8$-szorosra nagyítottunk. A közbeeső háromszögek nyilván szerkeszthetők is.   Megjegyzések. 1. Desargues egyik tétele azt mondja, hogy ha két háromszög olyan helyzetű, hogy egy‐egy szögpontját összekötő egyenesek egy ponton mennek át, akkor a megfelelő oldalak egy egyenesen metszik egymást és fordítva. (L Vigassy Lajos : Síkmértani szerkesztések térmértani megoldással. 66. ábra. Szakköri füzetek.) Példánkban a megfelelő oldalak párhuzamosak, tehát metszéspontjuk ideális pont. A három ideális pont a sík ideális egyenesén van, tehát a megfelelő csúcsokat összekötő egyenesek egy $\left(K\right)$ ponton mennek át. 2. Ha adva van két egyező körüljárású hasonló háromszög, akkor mindig csak egy olyan forgatva nyújtás létezik $\left(K\mathrm{,}\phi \mathrm{,}\lambda \right)$, amellyel az egyik a másikba átvihető. De ez mindig létezik is. Legyen ugyanis a két háromszög egy‐egy megfelelő oldala $A_1{B}_1$ és $A_4{B}_4$, az $\frac{A_4{B}_4}{A_1{B}_1}=\lambda =\frac{K{A}_4}{K{A}_1}$. Ez azt mondja, hogy a $K$ pontok mértani helye egy Apollonius‐féle kör. Továbbá $A_1{B}_1$ és $A_4{B}_4$ szöge nagyságra és irányra nézve megegyezik az $A_{1}K{A}_4$ szöggel. Az adott szög miatt a $K$ pont másik mértani helye az $A_1{A}_4$ ponton átmenő egyetlen körív. A kör és a körív mindig metszi egymást, és csak egy pontban. (Vigassy Lajos: Geometriai transzformációk. 44. ábra. Szakköri füzetek). 3. Alkalmazzunk egy $AB$ szakaszra egy $K_1$ pontból egy forgatva nyújtást, majd az így nyert eredményre egy $K_2$ pontból egy másik forgatva nyújtást. Bizonyítható, hogy azon forgatva nyújtás középpontja $\left(K_3\right)$, amely az eredeti szakaszt a harmadik helyzetbe átviszi, mindig rajta van a $K_1$ és $K_2$ pontokat összekötő egyenesen. (Lásd uo. 42. ábra.)    Vigassy Lajos