Kezdőlap


Feladat:	1176. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ágoston P. , Angyal J. , Bartha I. , Bisztray D. , Bruckner Lívia , Bökönyi T. , Csetényi A. , Csigi Márta , Donga Gy. , Gyimesi A. , Gyimesi F. , Gönczi I. , Hadik R. , Hegyi Gy. , Horváth L. , Horváth Mária , Kacsuk P. , Kálmán M. , Karády Ilona , Kiss Ipoly , Konkoly-Thege I. , Krasznai P. , Kuhár J. , Kökényesi Gy. , Lázár A. , Légrády G. , Lengyel J. , Lukács P. , Máté A. , Mezei I. , Morvai I. , Prőhle T. , Répási J. , Sailer K. , Simon Júlia , Szász T. , Székely Judit , Szendrei Mária , Szendrényi T. , Szlacsányi K. , Szőke Mária , Szolga L. , Sztrapkovics L. , Terlaky Edit , Tóth Ágnes , Tóth Tamás , Törő Judit , Török Gy. , Úry László , Varga G. , Várhegyi Éva
Füzet:	1969/április, 156 - 158. oldal		PDF \| MathML
Témakör(ök):	Síkidomok átdarabolása, Sokszögek szerkesztése, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/január: 1176. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen az eredeti nyolcszög centruma $O$ , egyik oldala $S T$ . A nyolcszög $S T$ oldalához csatlakozó oldalain az $O$ pont vetületét jelöljük $P$ -vel, illetve $R$ -rel. A nyolcszög forgásszimmetriája miatt $O P$ és $O R$ egyenlők és merőlegesek egymásra, ezért a $P S$ és $T R$ oldalak metszéspontját $Q$ -val jelölve $O P Q R$ négyzet. Jelöljük az $S T$ , $P R$ egyeneseknek $O Q$ -val alkotott metszéspontját $Q_{1}$ -gyel, illetve $Q_{2}$ vel. Legyenek végül a $Q_{1}$ , majd a $Q_{2}$ ponton át $P Q$ -val, illetve $R Q$ -val húzott párhuzamosoknak az $O P$ , $O S$ , $O T$ , $O R$ egyeneseken levő pontjai rendre $P_{1}$ , $S_{1}$ , $T_{1}$ , $R_{1}$ , illetve $P_{2}$ , $S_{2}$ , $T_{2}$ , $R_{2}$ . Ekkor a megszerkesztendő felbontás egy cikke az $O P_{1} S_{1} S T T_{1} Q_{2}$ sokszög, a további cikkeket ebből $O$ körüli, $45^{\circ}$ -os forgatásokkal kapjuk meg (2. ábra).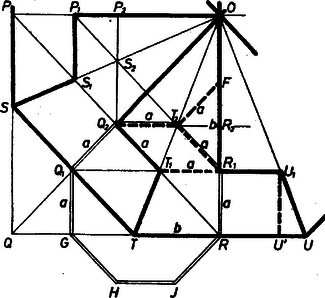

2. ábra

Valóban, az

O P_{1} S_{1} S

törött vonalat az

O

körüli forgatás az

O Q_{2} T_{1} T

törött vonalba viszi, hiszen a szerkesztés miatt az

O P

O S

O Q

O T

O R

egyenesek közti szögek rendre

{22, 5}^{\circ}

-osak. Továbbá

P S

és

S T

, tehát a velük párhuzamos

P_{1} S_{1}

S_{1} T_{1}

egyenesek is szimmetrikusak

O S

-re, tehát

O P_{1} = O Q_{2}

O S

és

O T

szimmetrikus

O Q

-ra, tehát

O S_{1} = O T_{1}

, végül

O S = O T

.
Az eredeti cikket az első forgatás az

O Q_{2} T_{1} T U U_{1} R

cikkbe viszi át, ennek feldarabolását az

U_{1}

ből

T U

-ra bocsátott merőlegessel, és a

T_{1} R_{1}

Q_{2} T_{2}

T_{2} R_{1}

és az

O Q

-val párhuzamos

T_{2} F

szakaszokkal végezzük el (

F

O R

egyenesen van).
Szerkesztésünk miatt az

R_{1} T_{2} F

háromszög egyenlő szárú derékszögű háromszög, hiszen

T_{2} R_{1} ∥ S T

T_{2} F ∥ O Q

. Jelöljük ennek a háromszögnek a befogóit

a

-val, átfogóját

b

-vel

(b = a \sqrt[]{2})

.
Az

O F T_{2}

háromszög egyenlő szárú, hiszen

T_{2} F ∥ O Q

és

O T

felezi a

Q O R

szöget, tehát

O F = a

. Mivel

O Q_{2} = O R_{1}

, az

O Q_{2}

szakasz hossza is

a + b

.
Az

O Q_{2} T_{2} F

négyszög egyenlő szárú trapéz, mert

T_{2} F ∥ O Q_{2}

, és az

O F

Q_{2} T_{2}

szárak egyaránt

45^{\circ}

-os szöget zárnak be az

O Q_{2}

alappal.
Az

R_{1} T_{2} Q_{2} T_{1}

négyszög szimmetrikus

O T

-re, és szemközti oldalai párhuzamosak, ez tehát rombusz, és oldalai

a

-val egyenlőek.
Az

O Q_{2} R

háromszög szimmetrikus a

Q_{2} R_{2}

tengelyre, tehát

R R_{1} = F O = a

.
Végül

Q_{1} T_{1} Q_{2}

is egyenlő szárú derékszögű háromszög, tehát egybevágó.

R_{1} F T_{2}

-vel.
Ezek szerint a

Q_{1} Q_{2} T_{2} R_{1} R

törött vonal egy

a

oldalú szabályos nyolcszög határvonalának a felét adja: ebbe a nyolcszögbe helyezzük bele az eredeti nyolcszög egy cikkének a darabjait.
Legyen

Q_{1}

vetülete

Q R

-en

G

. Mivel

G R = Q_{1} R_{1} = O R_{1} = a + b

, a

G R

szakaszra hézagmentesen rá tudjuk illeszteni a

Q_{2} O F T_{2}

trapéz

Q_{2} O

alapját, új helyzete a

G R

egyenes

O

-val ellentétes oldalán a

G R J H

trapéz. A

T U U_{1} T_{1}

trapézt az

U_{1}

-ből húzott magassága mentén elvágva, a kapott háromszöget hátlapjára fordítva és

T T_{1}

-hez illesztve téglalapot kapunk, és azt épp a

G R R_{1} Q_{1}

téglalapba tudjuk áttolni. Végül az

F T_{2} R_{1}

háromszöget a

T_{1} Q_{2} Q_{1}

háromszögre helyezzük, ezzel az állítást bebizonyítottuk.

Megjegyzések. 1. Tetszetősebb az átdarabolás, ha nem hozunk létre túl kicsi darabokat, mint itt az

U U_{1} U'

háromszög. Ez elkerülhető, ha a

T U U_{1} T_{1}

trapézt pl. az

R R_{1}

szakasz mentén vágjuk ketté.
2. Az éppen most mondott vágásvonalat véve, nincs szükség arra, hogy e részek egyikét a hátoldalára fordítsuk: tegyük

R U U_{1} R_{1}

-et

Q_{1} T T_{1} Q_{2}

-re és

F T_{2} R_{1}

-et

Q_{1} G T

-re. Ezzel a

T_{1} R_{1}

vágásvonal is feleslegessé válik.
3. Feleslegessé válik a

T_{1} Q_{2}

vágásvonal is, ha a nyolcszöget a kiindulásban az oldalakra merőleges szimmetriatengelyekkel osztjuk

8

egybevágó deltoidra. Ekkor az

Q Q_{1} T R

deltoidot csak

3

részre kell továbbosztanunk

T_{2} F

T_{2} Q_{2}

és

T_{2} R_{1}

mentén.
4. Mindezek a változtatások azonban egyre távolodnak jelenlegi feladatunktól, és visszahajlanak a (kitűzéskor is idézett) 1470. feladathoz. ¹ A 3. ábra a 3. megjegyzés eredményét továbbfejlesztve az

1 a

jelű darabot a két szomszédos deltoid

8 b

jelű trapézával, ill.

2 c

jelű háromszögével egészíti ki szabályos nyolcszöggé, így e darabok eredeti állásokban jutnak új helyükre (hasonlóan az 1470. feladat

3 h

ábrájához).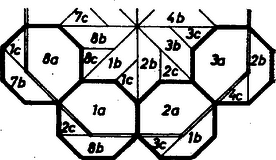

3. ábra

¹K. M. L. 35 (1967) 53. o.