Kezdőlap


Feladat:	1174. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Várhegyi Éva
Füzet:	1968/október, 72 - 73. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikus geometria síkban, Síkbeli szimmetrikus alakzatok, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1968/január: 1174. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel a megrajzolt átlók nem metszhetik egymást, a keletkezett háromszög csúcsaiként csak az adott $S_{9}$ szabályos kilencszög csúcsai szerepelhetnek. Ezért a háromszögek minden szöge $S_{9}$ valamelyik szöge vagy annak része lesz. Fordítva, $S_{9}$ minden szöge ‐ esetleg feldarabolva ‐ fellép valamelyik háromszögben. Így a háromszögek szögeinek $n \cdot 180^{\circ}$ összege ‐ ahol $n$ a keletkezett háromszögek száma ‐ egyenlő $S_{9}$ szögeinek összegével, ami viszont $7 \cdot 180^{\circ}$ ; ezért $S_{9}$ minden olyan háromszögelésében, melyben átlók nem metszik egymást, $n = 7$ háromszög keletkezik, tehát 6 átlót kell berajzolnunk.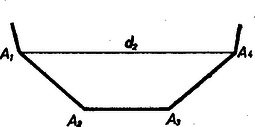
$S_{9}$ nek 3-féle átlója van, ti. az átlónak az $O$ középpontot nem tartalmazó oldalán 1, 2 vagy 3 lehet a lemetszett csúcsok száma; nevezzük ezeket rendre $d_{1}$ , $d_{2}$ , $d_{3}$ típusú átlónak.

1. ábra

A kívánt feldarabolásban nem léphet fel

d_{2}

típusú átló, mert ennek

O

-t nem tartalmazó oldalán egy négyszög állna, pl. az 1. ábrán

A_{1} A_{4} A_{3} A_{2}

, ezt a fentihez hasonló meggondolás szerint egyetlen további átló berajzolásával még fel kellene osztanunk két háromszögre, ekkor pedig

A_{2}

és

A_{3}

valamelyike 2, azaz páros számú háromszögnek lenne csúcsa, amit a feladat kizárt.

d_{3}

típusú átlóból legföljebb 2-t rajzolhatunk be úgy, hogy ne messék egymást, 2 egy csúcsból indulót; csak

d_{1}

típusú átlókra gondolva pedig legföljebb 4-et rajzolhatunk be, ezeknek páronként egymáshoz kell kapcsolódniuk,

S_{9}

-nek együttvéve 8 oldalát kell levágniuk. Így

d_{1}

és

d_{3}

típusú átlóból együttvéve legföljebb 6 rajzolható. Ezt előbbi eredményünkkel egybevetve kapjuk, hogy a kívánt felbontásban ‐ amennyiben az egyáltalán lehetséges ‐ két

d_{3}

és négy

d_{1}

típusú átlónak kell szerepelnie.
Mármost két, közös

C

csúcsból induló

d_{3}

típusú átló között egy háromszög, két oldalukon pedig egy‐egy ötszög keletkezik, és az utóbbiakba a további 2‐2

d_{1}

típusú átló berajzolása egyértelmű (2. ábra).

2. ábra

A kapott feldarabolás a két

d_{3}

típusú átló közti szög felezőjére szimmetrikus, másrészt

S_{9}

bármelyik csúcsa az előbb megválasztott

C

helyére fordítható úgy, hogy

S_{9}

a maga egészében önmagával fedésbe jusson, így további feldarabolás valóban nem lehetséges. Ezzel az állítást bebizonyítottuk.

Várhegyi Éva (Budapest, Berzsenyi D. Gimn., II. o. t.)

Megjegyzés. A feladat témája rokonságban áll az 1967. évi Kürschák‐verseny 2. feladatával.¹
Egy szabályos hétszög (további korlátozás nélküli) háromszögelésével foglalkozott az 1187. feladat.²

¹Lásd Hajós György: Az 1967. évi Kürschák József matematikai tanulóverseny feladatainak megoldása, K. M. L. 36 (1968) 193‐202. o.

²K. M. L. 26 (1963) 124‐127. o.