Feladat: 1167. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: könnyű
Megoldó(k):  Horváth Mária ,  Lengyel János 
Füzet: 1968/november, 142 - 143. oldal  PDF  |  MathML 
Témakör(ök): Körülírt kör, Húrnégyszögek, Gyakorlat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1967/december: 1167. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Az adott k kör OP sugara a POA és POB háromszögek közös oldala, ezért Ka, Kb rajta van OP-nek f felező merőlegesén, tehát az OKaPKb=N négyszög szimmetrikus f-re (deltoid), 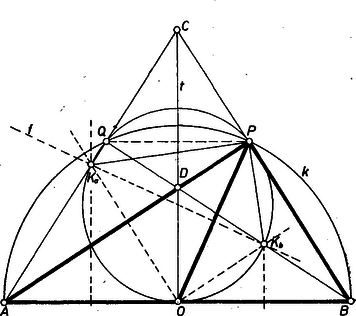KaOKb∢=KaPKb∢.
Másrészt a KaOKb szög két szára a k-beli PA, ill. PB húr felező merőlegese, ezért KaOKb∢=APB∢, ami a föltevés szerint derékszög. Így O, P rajta van a KaKb szakasz feletti Thalész-körön, tehát N húrnégyszög, az első állítást bebizonyítottuk.

 

 

b) Az AKa, BKb egyenesek metszéspontját Q-val jelölve elég belátnunk, hogy AQB∢ derékszög, vagy ‐ ami ugyanaz ‐ hogy a δ=QAB∢+QBA∢ összeg derékszög. Valóban, az OAKa és OBKb egyenlő szárú háromszögek, ezért
δ=KaOA∢+KbOB∢=AOB∢-KaOKb∢=180∘-90∘=90∘.
Felhasználtuk, hogy Ka, Kb az AB átmérőnek ugyanazon partján vannak, mint P. Ez helyes, mert a POA, POB háromszögek P-nél levő szöge hegyesszög.
 

Lengyel János (Budapest, I. István Gimn., I. o. t.)

Horváth Mária (Hódmezővásárhely, Liszt F. Ének-Zenei Ált. Isk., 7. o. t.)
 

Megjegyzések. 1. Az a) állítás így is bizonyítható: a középponti és kerületi szögek tétele alapján N-ben
OKaP∢+OKbP∢=2⋅OAP∢+2⋅OBP∢=2(BAP∢+ABP∢)=180∘,
mert ABP derékszögű háromszög. Felhasználtuk, hogy A és Ka az OP húrnak ugyanazon oldalán vannak, úgyszintén B és Kb is, mert PAO és PBO hegyesszögek.
2. A b) részben azt is beláthatjuk, hogy Q a P pont tükörképe AB felező merőlegesére nézve. Valóban
QAO∢=KaAO∢=KaOA∢=PBO∢,
mert KaO∥PB, hiszen mindkettő merőleges PA-ra.
 

II. megoldás. Az APB háromszög P-nél derékszögű. Ka-t és Kb-t származtathatjuk mint AP és AO, ill. BP és BO felező merőlegesének a metszéspontját. AP és BP felező merőlegese az ABP háromszögben az egyik, ill. másik befogóval párhuzamos középvonal. Felhasználva még, hogy AKaO és OKbB egyenlő szárú háromszögek, kapjuk, hogy
KaAO∢=KaOA∢=PBO∢ésKbBO∢=KbOB∢=PAO∢,
tehát az AKa és BKb egyenes BP-nek, ill. AP-nek tükörképe az AB szakasz t felező merőlegesére; így merőlegesek egymásra, Q metszéspontjuk az AB átmérőjű körön van, P tükörképe t-re. Ezzel igazoltuk a feladat második állítását.
Mivel a befogókkal párhuzamos középvonalak átmennek O-n, így a KaKb szakasz O-ból derékszögben látszik; végül Ka is, Kb is rajta van az AOP és BOP háromszögek közös OP oldalának felező merőlegesén, tehát O és P egymás tükörképei a KaKb egyenesre, így P is rajta van a KaKb átmérőjű körön. Ezzel a feladat első állítását is igazoltuk.
 

Megjegyzések. 1. A KaKb átmérőjű kör Q-n is átmegy, mert innen is derékszögben látszik KaKb, amennyiben Q és Ka különböző.
2. AKa-nak és BP-nek C metszéspontja, valamint BKb-nek és AP-nek D metszéspontja t-n van a bizonyított szimmetria miatt, és Ka felezi AC-t, Kb pedig BD-t, mert az AOC, ill. BOD háromszög t-vel párhuzamos középvonalán van.