Kezdőlap


Feladat:	1159. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1968/október, 66 - 67. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Tengelyes tükrözés, Hossz, kerület, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/november: 1159. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy az $A B C$ háromszög kerülete akkor a legnagyobb, ha $C$ az $A B D A' B' D' = H$ hatszög $A B$ -vel párhuzamos $A' B'$ oldalának valamelyik végpontjában van. Mivel az $A B$ oldal rögzített, elég az $A C + C B$ összeget vizsgálnunk; azt akarjuk tehát megmutatni, hogy

\begin{matrix} A C + C B < A A' + A' B', \end{matrix}

(1)

és egyenlőség csak akkor van, ha

C

A'

B'

pontok egyikével azonos. A szimmetria miatt elég azokra a

C

pontokra szorítkozni, amelyek a

H

idom

A B

-re merőleges

t

tengelyének

B

-t tartalmazó partján, vagy a tengelyen vannak.
Megoldásunk során a

C

pontot tetszőleges helyzetből kiindulva alkalmas mozgatással átvisszük az

A'

pontba úgy, hogy közben az

A C + C B

összeg fokozatosan növekedjék (ill. sohase csökkenjen). Legyen

c

C

-n átmenő,

A B

-vel párhuzamos egyenes, és messe ez a

B D A'

törött vonalat a

C_{1}

pontban. A

C

pontot előbb

c

mentén

C_{1}

-be, majd a

B D A'

törött vonal mentén

A'

-be mozgatjuk el.
Tükrözzük az

A

B

pontokat

c

-re, kapjuk rendre a

B_{1}

A_{1}

pont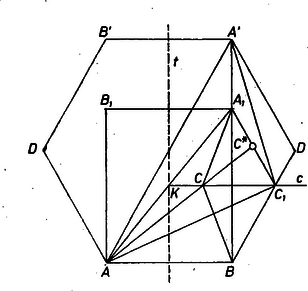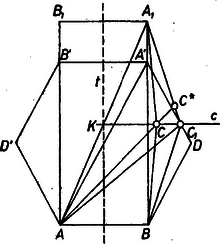okat.

A B A_{1} B_{1}

négyszögnek

c

és

t

szimmetriatengelye, e négyszög tehát téglalap, és az

A A_{1}

átló átmegy a tengelyek

K

metszéspontján. Mivel

C

K C_{1}

szakaszon van, az

A C

egyenes metszi az

A C_{1} A_{1}

háromszög

A_{1} C_{1}

oldalát, legyen e metszéspont

C^{*}

. Ha

C^{*}

A_{1} C_{1}

szakasz belső pontja, az

A_{1} C C^{*}

A C^{*} C_{1}

háromszögekre felírt háromszög-egyenlőtlenségek alapján

\begin{matrix} A C + C A_{1} < A C + C C^{*} + C^{*} A_{1} = A C^{*} + C^{*} A_{1} < A C_{1} + C_{1} C^{*} + C^{*} A_{1} = \\ = A C_{1} + C_{1} A_{1} . \end{matrix}

C^{*}

azonos az

A_{1}

ponttal, akkor az első egyenlőtlenség helyett egyenlőség áll, de a második egyenlőtlenség érvényes; ha pedig

C^{*}

C_{1}

ponttal azonos ‐ azaz

C

és

C_{1}

azonosak ‐, akkor mindkét egyenlőtlenség helyén egyenlőség áll. A tükrözés miatt

C A_{1} = C B

C_{1} A_{1} = C_{1} B

, így

\begin{matrix} A C + C B ≦ A C_{1} + C_{1} B, \end{matrix}

(2)

ahol egyenlőség csak akkor áll, ha

C

és

C_{1}

azonosak.
Mivel

A A'

H

köré írható kör átmérője,

A A' ≧ A C_{1}

, és egyenlőség csak

C_{1} = A'

mellett áll. Az

A' B C_{1}

háromszögben

C_{1}

-nél tompaszög van, hiszen ez a szög nagyobb a

120^{\circ}

-os

A' D B ∢

-nél; így

A' B > C_{1} B

, ha

C_{1}

nem azonos

A'

-vel. Ezek alapján

\begin{matrix} A C_{1} + C_{1} B ≦ A A' + A' B, \end{matrix}

(3)

ahol egyenlőség csak akkor van, ha

C_{1}

és

A'

azonosak. (2) és (3) együtt a bizonyítandó (1) egyenlőtlenséget adja, állításunk bizonyítását befejeztük.