Kezdőlap


Feladat:	1153. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Backhausz Beáta , Iglói Ferenc
Füzet:	1968/szeptember, 23 - 25. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Súlyvonal, Síkgeometriai számítások trigonometria nélkül háromszögekben, Diszkusszió, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/október: 1153. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a keresett háromszög derékszögének csúcsa $C$ -nél, a $C A$ , $C B$ befogók felezőpontja $B_{1}$ , ill. $A_{1}$ , és $A A_{1} = s_{a}$ , $B B_{1} = s_{b}$ az előírt súlyvonalak (1. ábra).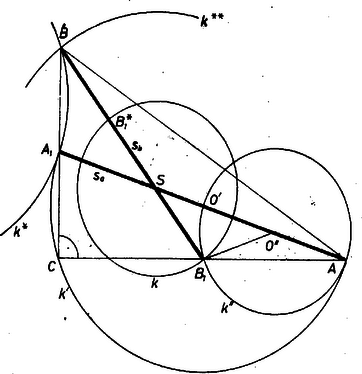

1. ábra

A A_{1}

helyzetét tetszés szerint megválasztva.

B_{1}

helyzetét két mértani helyből határozzuk meg. Az

S

súlypont ‐ harmadoló tulajdonságánál fogva ‐ kitűzhető, s ekkor

B_{1}

rajta van az

S

körül

s_{b} / 3

sugárral írt

k

körön. Másrészt

C

A A_{1}

átmérő fölötti,

O'

középpontú

k'

Thalész-kör pontja, ezért

B_{1}

azon a

k''

körön is rajta van, amelyet

k'

-ből kapunk az

A

középpontú, 1/2 arányú kicsinyítéssel.

B_{1}

ismeretében

C

-t

k'

-ből kimetszi az

A B_{1}

félegyenes, végül

B

C

-nek tükörképe az

A_{1}

pontra nézve.
Az így kapott

A B C

háromszög megfelel az előírásoknak, mert

A C B ∢ = A C A_{1} ∢

, derékszög,

A A_{1} = s_{a}

súlyvonal és

S

a súlypont, végül mivel

B_{1}

felezi az

A C

befogót,

B B_{1}

is súlyvonal, így átmegy

S

-en, és

B B_{1} = 3 \cdot S B_{1} = s_{b}

k

és

k''

általában 2 pontban metszik egymást, de a

B_{1}

helyzetére így adódó pontok egymás képei az

A A_{1}

tengelyre nézve, így legfeljebb 1 megoldása van a feladatnak.

k''

-nek

O''

középpontjára fennáll

A O'' = A O' / 2 = s_{a} / 4

. Az

S, O'', B_{1}

pontok valódi háromszöget alkotnak, ha

\begin{matrix} S O'' - B_{1} O'' < S B_{1} < S O'' + O'' B_{1}, \end{matrix}

azaz

O'' O' = O'' B_{1} = O'' A

figyelembevételével

\begin{matrix} S O' < S B_{1} < S A, \frac{s_{a}}{6} < \frac{s_{b}}{3} < \frac{2 s_{a}}{3}, \frac{s_{a}}{2} < s_{b} < 2 s_{a} . \end{matrix}

(1)

(A szimmetria miatt hasonló feltétel várható

s_{a}

két korlátjára; valóban a feltétel első feléből

s_{a} < 2 s_{b}

, a másodikból

s_{a} > s_{b} / 2

Megjegyzés.

B

B_{1}

pontból úgy is kiadódik, ha ezt előbb

S

-re tükrözzük (

B_{1}^{*}

), majd

S

-ből a 2-szeresére nagyítjuk. Ez adja a fenti szerkesztés következő változatát:

k'

tükörképe

A_{1}

-re

k^{*}

, az

S

körüli

2 s_{b} / 3

sugarú kör

k^{* *}

, és ekkor

B

k^{*}

és

k^{* *}

metszéspontja.
Iglói Ferenc (Szeged, Radnóti M. Gimn., I. o. t.)

II. megoldás (vázlat). A keresetthez hasonló háromszöget szerkeszthetünk egyszerű számítás alapján, ezt azután a kívánt nagyságra transzformáljuk. A szokásos jelölésekkel

\begin{matrix} s_{a}^{2} = \frac{a^{2}}{4} + b^{2}, s_{b}^{2} = \frac{b^{2}}{4} + a^{2}, \end{matrix}

ezekből

\begin{matrix} a^{2} = \frac{4}{15} (4 s_{b}^{2} - s_{a}^{2}), b^{2} = \frac{4}{15} (4 s_{a}^{2} - s_{b}^{2}), & (2) \\ a : b = \sqrt[]{4 s_{b}^{2} - s_{a}^{2}} : \sqrt[]{4 s_{a}^{2} - s_{b}^{2}} . \end{matrix}

2. ábra

A szerkesztést a 2. ábra vázolja. A négyzetgyökök szerkeszthető voltának feltétele azonos (1) aláhúzott részével. Itt nincs szükség harmadolásra.

Megjegyzések. 1. Kissé hosszabb a következő eljárás. (2) felhasználásával

\begin{matrix} c^{2} = a^{2} + b^{2} = \frac{4}{5} (s_{a}^{2} + s_{b}^{2}), c = \sqrt[]{\frac{2^{2}}{1^{2} + 2^{2}}} \cdot \sqrt[]{s_{a}^{2} + s_{b}^{2}}, \end{matrix}

(3)

vagyis az

s_{a}

s_{b}

befogókkal meghatározott derékszögű háromszög átfogóját egy 1 és 2 befogókkal szerkesztett derékszögű háromszög felhasználásával kicsinyítve megkapjuk

c

-t, ebből az

A B S

háromszöget, és azt kiegészítjük. A

\begin{matrix} \frac{2}{3} | s_{a} - s_{b} | < 2 \sqrt[]{\frac{s_{a}^{2} + s_{b}^{2}}{5}} < \frac{2}{3} (s_{a} + s_{b}) \end{matrix}

feltétel első fele mindenesetre teljesül, a második fele pedig akkor, ha

\begin{matrix} 2 s_{a}^{2} - 5 s_{a} s_{b} + 2 s_{b}^{2} = (2 s_{a} - s_{b}) (s_{a} - 2 s_{b}) < 0. \end{matrix}

Backhausz Beáta (Budapest, Ságvári E. Gyak. Gimn., III. o. t.)

2. A keresett háromszöghöz hasonlót szerkeszthetünk a következők alapján is (3. ábra).

3. ábra

B

-ből

A_{1} A

-val párhuzamosan húzott egyenes esse

C A

-t

B_{0}

-ban. Ekkor

C B_{0} = 2 C A = 4 C B_{1}

, és

B B_{0} = 2 A_{1} A = 2 s_{a}

. Ennek alapján egy derékszög egyik szárára

C B_{1}^{*}

C A^{*} = 2 C B_{1}^{*}

és

C B_{0}^{*} = 4 C B_{1}^{*}

távolságot mérünk, majd megszerkesztjük a másik szárnak azzal az Apollóniosz-körrel való

B^{*}

metszéspontját, amelynek pontjaira a

B_{1}^{*}

-től és

B_{0}^{*}

-tól való távolságok aránya

s_{b} : 2 s_{a}

. Végül az

A^{*} B^{*} C

háromszöget kellően nagyítjuk vagy kicsinyítjük.