Feladat: 1151. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bauer Katalin ,  Sándor Péter 
Füzet: 1968/március, 123 - 124. oldal  PDF  |  MathML 
Témakör(ök): Kombinatorikus geometria síkban, Szabályos sokszögek geometriája, Gyakorlat, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1967/október: 1151. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A továbbiakban, ha 2 pont közti körívet említünk más megjelölés nélkül, akkor ezen a rövidebb ívet értjük. Az Ö szabályos ötszög, ill. a H szabályos hétszög két szomszédos csúcsa közti ívet Ö-ívnek, ill. H-ívnek nevezzük. ‐ Bármelyik Ö-íven van csúcsa H-nak, mert ‐ a kör kerületét p-vel jelölve ‐ az Ö-ív hossza p/5, a H-ívé p/7,

p7<p5(<p2),(1)
nem lehet tehát, hogy egy H-ív magába zárjon egy Ö-ívet. Másrészt egy Ö-íven H-nak legföljebb két csúcsa lehet, mert 3 egymás utáni H-csúcs 2 H-ívet ad, és
2⋅p7>p5
miatt egy Ö-ív nem zárhat magába két, egymás utáni H-ívet.
Így Ö-nek 3 ívén 1‐1 csúcsa van H-nak, 2 ívén pedig 2‐2 csúcsa. Az utóbbi két Ö-ív nem szomszédos; ha ugyanis egymás utániak volnának, a rajtuk levő 4 H-csúcs 3 egymás utáni H-ívet adna, márpedig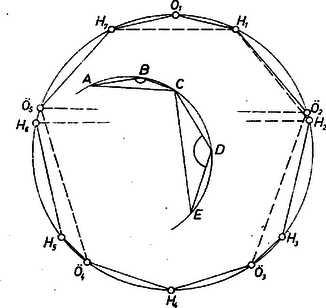
3⋅p7>2⋅p5.
 

 

Választhatjuk ezek alapján Ö és H csúcsainak indexelését úgy, hogy az Ö2Ö3 és Ö4Ö5 íveken legyen 2‐2 H-csúcs, H1 az Ö1Ö2 íven legyen, és az indexek ugyanabban a forgásirányban növekedjenek. Így a kérdéses T tizenkétszög egymás utáni csúcsai Ö1, H1, Ö2, H2, H3, Ö3, H4, Ö4, H5, H6, Ö5, H7.
T két szöge helyett elég összehasonlítanunk azt a két húrt, melynek végpontjai T-nek a szög csúcsával szomszédos csúcsai. Pl. a H7Ö1H1 és H1Ö2H2 szögek esetében H7H1=H1H2, mint H oldalai, így a körnek a két szög szárai közti ‐ félkörnél nagyobb ‐ H7H2H1 és H1H7H2 ívei egyenlők, ezért a mondott két szög is egyenlő, hiszen a mondott íveken nyugvó kerületi szögek. Ugyanígy T-nek mindegyik Ö1(i=1, 2, 3, 4, 5) csúcsnál levő szöge ugyanakkora.
Általában hasonlóan, ha A, B, C, D, E egy félkörnél kisebb körívnek egymás utáni pontjai, és AC<CE, akkor ABC∢>CDE∢, mert az ABC ív kisebb a CDE ívnél, így a B-t nem tartalmazó AC ív nagyobb, mint a D-t nem tartalmazó CE ív. Ha pedig AC=CE, akkor ugyanígy ABC∢=CDE∢.
Eszerint T-ben a H1, H4, H7 csúcsoknál is egyenlő szögek vannak, továbbá pl. Ö1H1Ö2∢<H7Ö1H1∢, mert (1)-ből Ö1Ö2>H7H1. Hátra vannak a H2, H3, H5, H6 csúcsnál levő szögek. Mindezek az előbbi kétféle szögnagyságtól különböző, és nagyságra nézve közéjük eső szögek, mert pl. Ö2H3 és H2Ö3 a H2H3-nál nagyobb, Ö2Ö3-nál viszont kisebb (tehát félkörnél is kisebb) ívek, ezért ugyanez áll a végpontjaik közti húrokra is.
Továbbá e 4 szög egymástól is különböző. A H2∢-et a többi három bármelyikével egyenlőnek véve ellentmondásra jutunk. H2∢=H3∢ esetén Ö2 és H3, valamint Ö3 és H2 egyenlő húrok és ívek végpontjai, az utóbbiakból közös részüket, a H2H3 ívet elhagyva Ö2H2 és Ö3H3 is egyenlő ívek, így pedig az Ö2Ö3 és H2H3 húrok párhuzamosak, és közös felező merőlegesük Ö-nek és H-nak közös szimmetriatengelye, a föltevéssel ellentétben. (Egyszersmind a szemben levő Ö5 és H6 egybeesnék.) Ugyanígy adódik H5∢=H6∢-ből H5H6∥Ö4Ö5.
Hasonlóan a H2∢=H6∢ föltevésből (és H3∢=H5∢-ből is) Ö2H3=Ö5H5, Ö2H2=Ö5H6, H2H6∥Ö2Ö5 következnék.
Végül a H2∢=H5∢ (és H3∢=H6) föltevésből Ö2H3=Ö4H6 mindkét oldalhoz hozzáadva a köztük levő H3Ö4 ívet, Ö2Ö4=H3H6, azaz 2p/5=3p/7 következik, ami nem igaz.
Mindezek szerint T szögei között 6 különböző érték fordul elő.
 

  Bauer Katalin (Budapest, Berzsenyi D. g. II. o. t.)
  Sándor Péter (Pannonhalma, Bencés g. I. o. t.)