Kezdőlap


Feladat:	1135. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Backhausz Beáta , Bajmóczy E. , Bálványos Z. , Bogár D. , Cserha Gabriella , Csobádi Péter , Ésik Z. , Eteli F. , Fiala T. , Fialovszky Alice , Fischer Ágnes , Fuggerth E. , Füredi A. , Gádoros Gabriella , Gajdács Ibolya , Győry F. , Gönczi I. , Hadik R. , Hárs L. , Horváth László , Kaján L. , Kemény A. , Kéthelyi J. , Lempert L. , Lengyel Erzsébet , Maróti P. , Martoni V. , Mihály Gy. , Móricz P. , Nagy Dénes , Nagy Zoltán , Németh K. , Nikodémusz Anna , Papp Zoltán , Pataki István , Pataki János , Pintér Vera , Sailer K. , Schván P. , Siklósi M. , Simon Júlia , Somogyi Á. , Somorjai G. , Szabó László Sándor , Tél T. , Turi A. , Törő J. , Váli L. , Váradi Judit , Zöldy B.
Füzet:	1968/április, 166 - 168. oldal		PDF \| MathML
Témakör(ök):	Vetítések, Paralelogrammák, Síkgeometriai szerkesztések, Helyvektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/május: 1135. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Szerkesztésünket az adott három ponttal meghatározott $S$ síkban végezzük. Legyen $D$ a sík egy az előírt tulajdonsággal bíró pontja, és tekintsük a rajta átmenő egyenesek közül azt, amelyik merőleges az $A C$ egyenesre; legyen ez $d_{1}$ . Ekkor $A$ és $C$ merőleges vetülete azonos $d_{1}$ és az $A C$ egyenes metszéspontjával, így (1) szerint $D B' = 0$ . Ez azt jelenti, hogy $B$ vetülete $d_{1}$ -re $D$ , vagyis $B D ⊥ d_{1} ⊥ A C$ , tehát $D$ csak az $A C$ -vel $B$ -n át húzott $e_{1}$ párhuzamos egyenes valamely pontja lehet.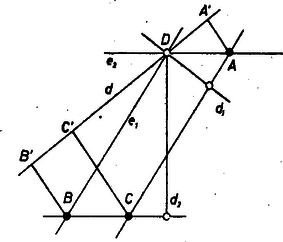

1. ábra

Ugyanígy adódik a

D

-n átmenő és

B C

-re merőleges

d_{2}

egyenes felhasználásával, hogy

D

csak a

B C

-vel

A

-n át húzott

e_{2}

párhuzamos egyenes pontja lehet.

e_{1}

és

e_{2}

különbözők, mert

A

B

C

háromszöget alkotnak, tehát egyetlen közös pontjuk van, az, amely az adott pontokat olyan paralelogrammává egészíti ki, melyben

C D

átló.
Megmutatjuk, hogy (1) teljesül bármely a

D

-n átmenő (

S

-beli)

d

egyenesre. Valóban, mivel

B C

párhuzamos, egyirányú és egyenlő

D A

-val, azért ugyanezek fennállnak

B' C'

és

D A'

között. Így az irányokat is figyelembe véve mindig fennáll

\begin{matrix} D A' = B' C' = B' D + D C' = - D B' + D C', \end{matrix}

amihez mindkét oldalon hozzáadva a

D B'

vektort, (1)-et kapjuk.

Papp Zoltán (Debrecen, Fazekas M. g. II. o. t.)

II. megoldás. Legyen ismét

D

egy a kívánt tulajdonsággal bíró pont,

d

egy rajta átmenő egyenes, továbbá

\vec{D A} = a

\vec{D B} = b

\vec{D C} = c

, és bontsuk fel az (1)-ben fellépő vektorokat 2‐2 vektor összegére

\begin{matrix} \vec{D C}' = c + \vec{C C}', \vec{D A}' = a + \vec{A A}', \vec{D B}' = b + \vec{B B}' . \end{matrix}

Ezekkel teljesül (1), amiből átrendezéssel

\begin{matrix} \vec{C C}' - \vec{A A}' - \vec{B B}' = a + b - c . \end{matrix}

(2)

d

egyenest

D

körül forgatva ennek a vektoregyenlőségnek a jobb oldala állandó, a bal oldal viszont változó; hiszen mindig merőleges

d

-re. Ez az ellentmondás csak úgy oldódik fel, ha a bal oldal

0

-vektor, csak így marad állandó, irányának megváltozása ellenére. Ekkor viszont a jobb oldalra is fennáll

\begin{matrix} a + b - c = 0, átrendezve c = a + b, azaz \vec{D C} = \vec{D A} + \vec{D B} . \end{matrix}

Ezt a bármely

D

pontra fennálló

\vec{D C} = \vec{D B} + \vec{B C} = \vec{D A} + \vec{A C}

egyenlőségekkel egybevetve

D

csak olyan pont lehet, melyre

\vec{D A} = \vec{B C}

és

\vec{D B} = \vec{A C}

, vagyis

\vec{A D} = \vec{C B}

és

\vec{B D} = \vec{C A}

, tehát

D

A

C

B

pontokat paralelogrammává kiegészítő pont, ha a paralelogrammában

C D

A B

az átlók.

Csobádi Péter (Budapest, Berzsenyi D. g. II. o. t.)

Megjegyzések. 1. Szerkesztésünk akkor is érvényes, ha

A

B

C

egy egyenesbe esnek, ekkor azonban (1) lényegében semmitmondó (2. ábra).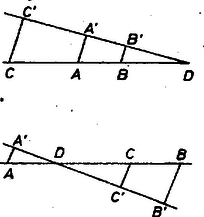

2. ábra

2. Akkor is érvényes (1), ha mindhárom pont vetítése egymással párhuzamosan történik a felvett egyeneshez tetszés szerinti szöggel hajló irányban.
3. Be lehet látni, hogy bizonyításunk a

D

-n átmenő, de nem az

A B C

síkban fekvő egyenesekre is érvényes.