Kezdőlap


Feladat:	1129. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bálványos Z. , Csobádi P. , Fuggeth Endre , Greskovits József , Gulyás András , Gulyás Imre , Hárs L. , Lempert L. , Morvai I. , Nagy Dénes , Pap Márta , Papp Z. , Somorjai G. , Szendrényi T. , Takács L. , Tóth Tibor , Váradi Judit
Füzet:	1968/február, 68 - 71. oldal		PDF \| MathML
Témakör(ök):	Mértani közép, Háromszögek hasonlósága, Síkgeometriai számítások trigonometria nélkül körökben, Diszkusszió, Síkgeometriai szerkesztések, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/április: 1129. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. 1. Ha $a = c$ , akkor $b$ átmérő és a szerkesztés magától értetődő. Ha $a \neq c$ , válasszuk a betűzést úgy, hogy a két szélső húr közül $a$ legyen a kisebbik: $a < c$ (1. áb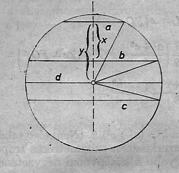ra).

1. ábra

Ekkor

c

közelebb van a velük párhuzamos

d

átmérőhöz, mint

a

, ezért

b

mindenesetre azon a partján van

d

-nek, mint

a

. Legyen

a

és

b

közti távolság

x

, az

a

és

d

közti távolság

y

, ekkor

d

-től a

b

húr

y - x

, a

c

húr pedig

| y - 2 x |

távolságra van. Pitagorasz tétele alapján

\begin{matrix} {(\frac{d}{2})}^{2} = y^{2} + {(\frac{a}{2})}^{2}, & (1) \\ {(\frac{d}{2})}^{2} = {(y - x)}^{2} + {(\frac{b}{2})}^{2}, & (2) \\ {(\frac{d}{2})}^{2} = {(y - 2 x)}^{2} + {(\frac{c}{2})}^{2} . & (3) \end{matrix}

Innen

y

-t és

d

-t kiküszöbölhetjük úgy, hogy kivonjuk (1) és (3) összegéből (2) kétszeresét:

\begin{matrix} 0 = {(\frac{a}{2})}^{2} + {(\frac{c}{2})}^{2} + 2 x^{2} - 2 {(\frac{b}{2})}^{2}, \\ 2 x = \sqrt[]{b^{2} - \frac{a^{2} + c^{2}}{2}}, & (4) \end{matrix}

ekkora az

a

és

c

húr távolsága.
2. A szerkesztés a következő.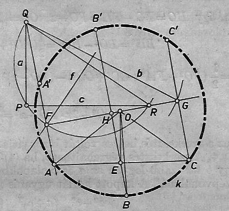

2. ábra

Egy

P

csúcsú derékszög (2. ábra) két szárára felmérjük

P Q = a

, ill.

P R = c

szakaszt, a

Q R

szakasz fölé Thalész-félkört írunk, kijelöljük rajta a szakasz

f

felező merőlegesén levő

F

pontot (

f

-et már a középpont szerkesztésében használtuk), az

F R

félegyenest metsszük a

Q

körüli

b

sugarú körrel a

G

pontban. Fölmérjük az

F Q

egyenesre az

F A = F A' = a / 2

, valamint a vele párhuzamos,

G

-n átmenő egyenesre a

G C = G C' = c / 2

szakaszt, ekkor a keresett

k

kör

O

középpontját az

A C

szakasz felező merőlegese metszi ki

F G

-ből, sugara pedig

O A

.
3. A szerkesztésből nyilvánvaló, hogy

A A'

C C'

k

-nak párhuzamos és

a

, ill.

c

hosszúságú húrja, mert merőlegesek

F G

-re; azt kell csak bebizonyítanunk, hogy az

A C

-nek

E

felezőpontján át velük párhuzamosan húzott ‐ és így

F A

-tól és

G C

-től egyenlő távolságra levő ‐

e

egyenes

k

-ból

b

hosszúságú húrt metsz ki. Legyen a húr

B B'

, felezőpontja

H

.
A szerkesztés szerint

Q R^{2} = a^{2} + c^{2}

Q R F

egyenlő szárú derékszögű háromszög, így

Q F^{2} = (a^{2} + c^{2}) / 2

, tehát

F G = 2 x

, megfelel (4)-nek.

O

H G

félegyenesen van, így

H O = F O - F H = F O - x

O G = | 2 x - F O |

. Mármost

\begin{matrix} B H^{2} = B O^{2} - H O^{2} = \frac{1}{2} (A O^{2} + C O^{2}) - {(F O - x)}^{2} = \\ = \frac{1}{2} (F O^{2} + F A^{2} + G C^{2} + O G^{2}) - {(F O - x)}^{2} = \frac{1}{2} (\frac{a^{2} + c^{2}}{4} + F O^{2} + {(2 x - F O)}^{2}) - \\ - F O^{2} + 2 x \cdot F O - x^{2} = \frac{a^{2} + c^{2}}{8} + x^{2} = \frac{b^{2}}{4}, \end{matrix}

és ez a szerkesztés helyes voltát bizonyítja.
4. A szerkesztés végrehajtható, ha (4)-ben

b^{2} > (a^{2} + c^{2}) / 2

. (Nem elég tehát, hogy

b

hosszabb legyen

a

és

c

alapokból szerkesztett szimmetrikus trapéz középvonalánál. A kapott korlát ugyanis nagyobb a középvonal négyzeténél:

\begin{matrix} \frac{a^{2} + c^{2}}{2} - {(\frac{a + c}{2})}^{2} = (\frac{{(a - c)}^{2}}{2} \geq 0) . \end{matrix}

A feltétel teljesülése esetén

1

megoldást kapunk.
Fuggert Endre (Budapest, Fazekas M. gyak. g. II. o. t.)

II. megoldás. 1. Legyenek a húrok rendre

A A'

B B'

C C'

, és messe

B B'

A C

-t

K

-ban,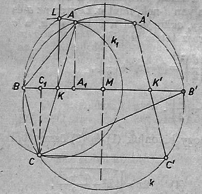

A' C'

-t

K'

-ben (3. ábra).

3. ábra

A B K

és

B' C K

háromszögek hasonlók, mert szögeik páronként egyenlők, így

\begin{matrix} \frac{B K}{K A} = \frac{C K}{K B'} = \frac{K A}{K B'}, & (5) \\ K A^{2} = K B \cdot K B', \end{matrix}

azaz

K A

mértani középarányos

B K

és

K B'

között. Másrészt

K K'

C C' A' A

trapéz középvonala, és az alakzat szimmetrikus a húrok közös felező merőlegesére, mint tengelyre nézve.
2. Ezek alapján a szerkesztés a következő. A

B B' = b

szakasz

M

felezőpontjától

B

felé fölmérjük az

M A_{1} = a / 2

M C_{1} = c / 2

szakaszokat.

A_{1}

-ben és

A_{1} C_{1}

-nek

K

felezőpontjában merőlegest rajzolunk

B B'

-re és az utóbbit metsszük a

B B'

átmérő fölötti Thalesz-körrel az

L

pontban. Ekkor a

K

körüli,

K L

sugarú

k_{1}

kör az előbbi merőlegesből kimetszi

A

-t,

A K

-nak

k_{1}

-gyel való másik metszéspontja

C

és a keresett

k

kör az

A B C

háromszög köré írt kör.
3. Bizonyításul elég azt megmutatnunk, hogy

k

átmegy

B'

-n is. Ekkor ugyanis az

M

-ben

B B'

-re állított

m

merőleges szimmetriatengelye

k

-nak, ezért

A

-nak és

C

-nek

m

-re vetett

A'

, ill.

C'

tükörképe is rajta van

k

-n,

A A'

és

C C'

párhuzamosak

B B'

-vel, mert merőlegesek

m

-re,

A A' = 2

M A_{1} = a

C C' = 2

M C_{1} = c

‐ ugyanis

C C_{1} ⊥ B B'

, hiszen a

C K C_{1}

háromszög egybevágó az

A K A_{1}

derékszögű háromszöggel ‐, végül ugyanezért

B B'

egyenlő távolságra van

A A'

-től és

C C'

-től. ‐ Állításunk abból következik, hogy

K L = K A

az ismert mértani középarányos szerkesztés miatt teljesíti (5) jobb oldali egyenlőségét, ezért a bal oldali egyenlőség is fennáll, így a

K

-nál egyenlő (csúcs-) szögekkel bíró

K A B

K C B'

háromszögek hasonlók,

B B' C ∢ = B A C ∢

.
4. A szerkesztés végrehajtható, ha

K L > K A_{1}

, azaz ‐ pozitív szakaszokról lévén szó ‐, ha

K L^{2} > K A_{1}^{2}

\begin{matrix} K B \cdot K B' = (\frac{b}{2} - \frac{a + c}{4}) (\frac{b}{2} + \frac{a + c}{4}) > K A_{1}^{2} = {(\frac{a + c}{4} - \frac{a}{2})}^{2}, \\ \frac{b^{2}}{4} - {(\frac{a + c}{4})}^{2} - {(\frac{c - a}{4})}^{2} = \frac{1}{4} (b^{2} - \frac{a^{2} + c^{2}}{2}) > 0, \end{matrix}

ami azonos feltétel az I. megoldásban találttal. A feltétel teljesülése esetén egyetlen

L

és (lényegében egyetlen)

A

pontot kapunk.
Greskovits József (Budapest, Könyves Kálmán g. II. o. t.)