Kezdőlap


Feladat:	1119. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Fuggerth E. , Goda B. , Hárs L. , Kardos J. , Lempert L. , Lengyel T. , Lőrincz A. , Lőrincz András , Nagy D. , Pataki János , Perémy G. , Simon Júlia , Takács L. , Takács László
Füzet:	1968/április, 158 - 162. oldal		PDF \| MathML
Témakör(ök):	Kombinatorikus geometria síkban, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/március: 1119. matematika gyakorlat

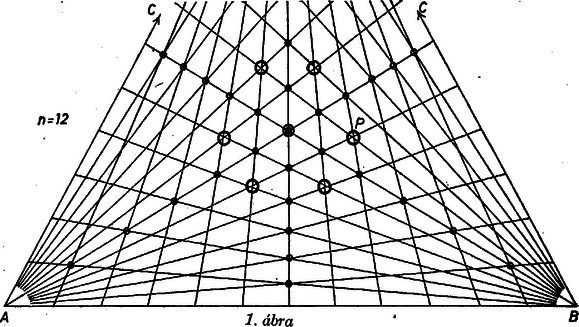
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Amikor az oldalakat 12‐12 részre osztjuk, egyik-egyik csúcsból 11 összekötő szakasz indul ki ‐ nevezzük ezeket transzverzálisoknak ‐, ezek egymás között nem adnak metszést. Viszont pl. egy az $A$ csúcsból kiinduló transzverzális metszi a $B$ -ből és $C$ -ből kiinduló transzverzálisok mindegyikét. Így mindegyik csúcs-pár transzverzálisai $11^{2}$ esetben metszik egymást, a $3$ csúcspárt tekintve $3 \cdot 11^{2} = 363$ esetben. Minthogy azonban a transzverzálisok között szerepel a szabályos háromszög mindhárom szimmetriatengelye, és a tengelyre szimmetrikus transzverzálisok a tengelyen metszik egymást, azért mindegyik tengelyen a $2 \cdot 11$ áthaladás csupán $11$ metszéspontot ad, köztük a háromszög középpontját is, ahol a 3 tengely metszi egymást. Így $3 (11 - 1) + 1 = 31$ hármas metszést találtunk, ezeket a $363$ metszésben 2-szer $- 2$ -szer fölöslegesen vettük számba.

Nincs további olyan metszéspont, amelyen 3 transzverzális haladna át. Ugyanis csak

6

transzverzális-hármas esetében esnek a metszéspontok annyira közel egymáshoz (pl. az 1. ábra

P

-vel jelölt helyén), hogy ‐ a természetesen adódó pontatlanság miatt ‐ kétséges, három külön metszésről van-e szó, vagy egyetlen hármas metszésről; azonban a

P

hely környezetében éppen az 1437. feladatban vizsgált transzverzális-hármas halad át, a többi

5

pedig belőle tengelyes tükrözéssel vagy a háromszög

120^{\circ}

-os elfordításával adódik, eszerint páronként különböző pontokban metszik egymást.
Eszerint a metszéspontok száma

363 - 2 \cdot 31 = 301

II. Az oldalakat 13‐13 egyenlő részre osztó transzverzálisok között nem szerepelnek a háromszög szimmetriatengelyei.

3

-as metszés létezése csak a 2. ábra

Q

-val és

R

-rel jelölt helyein kétséges.

2. ábra

Ezeken a helyeken az 1437. feladathoz fűzött megjegyzés jelöléseivel (3. ábra) alkalmas egységben

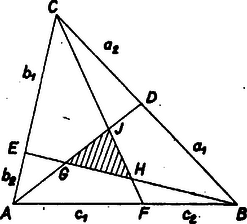3. ábra

\begin{matrix} a_{1} & a_{2} = 13 - a_{1} & b_{1} & b_{2} = 13 - b_{1} & c_{1} & c_{2} = 13 - c_{1} \\ Q & 2 & 11 & 12 & 1 & 4 & 9 \\ R & 4 & 9 & 12 & 1 & 2 & 11 \end{matrix}

így az ugyanott nyert

\begin{matrix} \frac{G H J}{A B C} = \frac{{(a_{1} b_{1} c_{1} - a_{2} b_{2} c_{2})}^{2}}{(a_{1} b_{1} + a_{1} b_{2} + a_{2} b_{2}) (b_{1} c_{1} + b_{1} c_{2} + b_{2} c_{2}) (c_{1} a_{1} + c_{1} a_{2} + c_{2} a_{2})} \end{matrix}

(1)

területarány-képlet felhasználásával mind a két kérdéses transzverzális-hármasra

a_{1} b_{1} c_{1} - a_{2} b_{2} c_{2} = - 3 \neq 0

, nincs hármas metszés.
Így a transzverzálisok a fenti meggondoláshoz hasonlóan

3 {(13 - 1)}^{2} = 432

különböző metszéspontot határoznak meg.

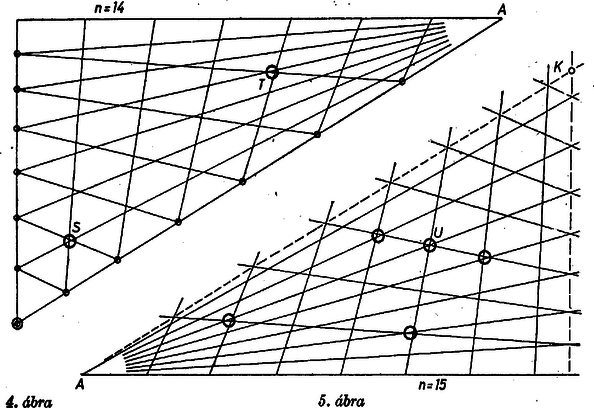
III. A 14 részre osztás esete lényegében azonos a 12 részre osztás esetével, a metszéspontok száma

3 {(14 - 1)}^{2} - 2 (3 (14 - 2) + 1) = 433

, ugyanis a 4. ábra

S

-sel és

T

-vel jelölt, kétséges helyén a transzverzális -hármasokra

a_{1} b_{1} c_{1} - a_{2} b_{2} c_{2} =

= 6 \cdot 9 \cdot 6 - 8 \cdot 5 \cdot 8 = 4

, ill.

3 \cdot 13 \cdot 3 - 11 \cdot 1 \cdot 11 = - 4

, egyik sem

0

IV. A 15 részre osztás esete viszont a 13 részre osztás esetéhez hasonló. Itt azonban az 5. ábra

U

helyén a transzverzális-hármas egy pontban metszi egymást, ugyanis

a_{1} = 5

a_{2} = 10

b_{1} = 12

b_{2} = 3

c_{1} = 5

c_{2} = 10

, és így

a_{1} b_{1} c_{1} - a_{2} b_{2} c_{2} = 0

. (A többi jelölt helyen nincs hármas metszés.) Így a különböző metszéspontok száma

3 {(15 - 1)}^{2} - 2 \cdot 6 = 576

Takács László (Sopron, Széchenyi I. g. III. o. t.)
Lőrincz András (Budapest, Kölcsey F. g. II. o. t.)

II. megoldás (vázlat). Célhoz érhetünk ábrák szemlélete nélkül, a hármas metszéspontok esetén teljesülő

a_{1} b_{1} c_{1} = a_{2} b_{2} c_{2}

feltétel alapján is. Az oldalanként keletkezett

n

egyenlő rész, azaz

n - 1

osztópont és transzverzális esetére a metszéspontok száma a fentiekhez hasonlóan

\begin{matrix} N = 3 {(n - 1)}^{2} - 2 H, \end{matrix}

ahol

H

a hármas metszéspontok száma, más szóval az (1)-ből adódó

\begin{matrix} a_{1} b_{1} c_{1} - (n - a_{1}) (n - b_{1}) (n - c_{1}) = 0, \end{matrix}

(2)

más alakban

\begin{matrix} n^{2} - (a_{1} + b_{1} + c_{1}) n + (a_{1} b_{1} + b_{1} c_{1} + c_{1} a_{1}) = \frac{2 a_{1} b_{1} c_{1}}{n} \end{matrix}

(3)

egyenletet kielégítő

a_{1}

b_{1}

c_{1}

természetes számhármasok száma. A fentiek szerint páros

n

esetére a háromszög tengelyein levő hármas metszéspontok száma ^{$^{*}$}

3 (n - 2) + 1 = 3 n - 5

, a továbbiak

6

-osával egymás szimmetrikus társai, ezért elég a

\begin{matrix} 0 < a_{1} < \frac{n}{2}, \frac{n}{2} < b_{1} < n, 0 < c_{1} < \frac{n}{2} \end{matrix}

(4)

további korlátozásnak eleget tevő megoldásokat keresnünk, így minden

6

-ost egyszer kapunk meg.

n = 13

esetén (3) jobb oldala nem lehet egész, mert

13

törzsszám (bal oldala viszont egész), nincs megoldás. Ugyanígy

n = 14 = 2 \cdot 7

esetén sem, mert a jobb oldal számlálójában (4) miatt nem léphet föl

7

-tel osztható tényező.

n = 12 = 2^{2} \cdot 3

esetén

a_{1} b_{1} c_{1}

-nek oszthatónak kell lennie

6

-tal, így (4)-re tekintettel

a_{1}

b_{1}

c_{1}

közül egyiknek párosnak kell lennie és egy másiknak

3

-mal oszthatónak. Az előbbi

2

4

8

vagy

10

lehet, az utóbbi

3

vagy

9

a_{1}

és

c_{1}

szimmetrikus szerepére tekintettel a következő alakú számhármasok jönnek tekintetbe:

\begin{matrix} (2, 9, c_{1}), (4, 9, c_{1}), (3, 8, c_{1}), (3, 10, c_{1}), \\ (2, b_{1}, 3), (4, b_{1}, 3), \end{matrix}

de az ezekkel (2)-ből adódó

\begin{matrix} c_{1} = \frac{n (n - a_{1}) (n - b_{1})}{a_{1} b_{1} + (n - a_{1}) (n - b_{1})}, ill. b_{1} = \frac{n (n - a_{1}) (n - c_{1})}{a_{1} c_{1} + (n - a_{1}) (n - c_{1})} \end{matrix}

egyik esetben sem egész.
Hasonlóan

n = 15 = 3 \cdot 5

esetén

a_{1} b_{1} c_{1}

-nek oszthatónak kell lennie

15

-tel, (4)-re tekintettel egyik tényezőnek

3

-mal, egy másiknak

5

-tel kell oszthatónak lennie. A szóba jövő

\begin{matrix} (3, 10, c_{1}), (6, 10, c_{1}), (5, 9, c_{1}), (5, 12, c_{1}), \\ (3, b_{1}, 5), (6, b_{1}, 5) \end{matrix}

alakú számhármasok közül az elsővel (3)-ból

c_{1} = 10

, ezt azonban (4)-ben kizártuk, a negyedikkel

c_{1} = 5

(az ebből és a kizárt

(3, 10, 10)

számhármasból adódó hármas metszéspontok egymás tükrös párjai a

C

-ből induló szimmetriatengelyre. Eszerint

n = 15

esetén

6

hármas metszéspont van.

Pataki János (Budapest, Berzsenyi D. g. I. o. t.)

Megjegyzések. 1. Az 1437. feladathoz fűzött megjegyzés mutatja, hogy megállapításaink tetszés szerinti alakú háromszögben is érvényesek.
2. Néhányan megpróbálkoztak azon az ábrán megszámlálni a metszéspontokat, amely

n

vizsgált négy értéke esetének egyesítésével adódik, de lényegében csak részeredményeket értek el. Néhány olyan hármas metszéspont, amelyen különböző

n

-értékekhez tartozó transzverzálisok mennek át:

\begin{matrix} a_{1} : a_{2} = 1 : 2, b_{1} : b_{2} = 11 : 2, c_{1} : c_{2} = 4 : 11; \\ = 5 : 7, = 8 : 5, = 7 : 8; \\ = 5 : 8, = 4 : 1, = 2 : 5. \end{matrix}

a_{1} : a_{2} = 1 : 2

osztópont

n = 12

és

n = 15

esetén is szerepel: 3. Az (1) képlet szerint a vizsgált

Q

R

S

T

hely környezetében áthaladó transzverzális-hármasokkal határolt háromszög területe az

A B C

háromszög területének rendre

\begin{matrix} 1 / 94 979, 1 / 141 486, 1 / 190 402, ill. 1/104 208 \end{matrix}

része. Az ilyen ,,majdnem egy pontban metsződő'' transzverzális-hármasok jellemzésére azonban célszerűbb lenne a háromszög legnagyobb oldalát megadni a területe helyett. Ezen az úton jutottunk megoldáshoz az 1437. feladat I. megoldásában.

^{$^{*}$}Eszerint tetszés szerinti

n

esetén

\begin{matrix} N \leq 3 {(n - 1)}^{2} - 2 ([\frac{n}{2}] - [\frac{n - 1}{2}]) (3 n - 5), \end{matrix}

ahol a szögletes zárójel a benne álló szám egész részét jelöli; ugyanis ezen egész részek különbsége páros

n

esetén

1

, páratlan

n

esetén

0