Feladat: 1112. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1967/november, 154 - 155. oldal  PDF  |  MathML 
Témakör(ök): Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Körülírt kör, Középponti és kerületi szögek, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):Feladatok: 1967/február: 1112. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Rajzoljunk kört a háromszög köré és húzzuk meg C-ben a t érintőjét. Ez az a oldallal α szöget, a b oldallal β szöget zár be, így acosα és bcosβ az a, ill. b vetülete t-n. (1) tehát azt jelenti, hogy C-től mindkét irányban alkalmas egyenlő távolságot mérve t-re, az ezekben t-re állított merőleges metszi ki A-t, ill. B-t a körből (1. ábra).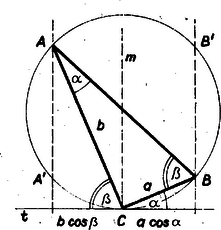

 
 
1. ábra
 

A két merőleges vagy érinti a kört, ekkor ABC egyenlő szárú derékszögű háromszög, vagy egy-egy húrt metsz ki, amelyek szimmetrikusak a C-ben t-re állított m merőlegesre. Így 4 pontot metszenek ki, amelyek egy téglalap csúcsai. A és B tehát vagy szimmetrikusak m-re, és ekkor AC=CB, a háromszög egyenlő szárú, vagy a téglalap átellenes csúcsai. Utóbbi esetben AB a kör egy átmérője (a téglalap másik két csúcsából derékszögben látszik), s így ABC háromszög C-nél derékszögű. (1) mindkét esetben valóban teljesül, utóbbiban azért, mert a C-ben t-re állított merőleges az érintési sugár, így felezi AB-t, AC és BC vetülete tehát AB egyik, ill. másik felének is vetülete.
 

Megjegyzések. 1. A feladat kitűzésekor a versenyzők még csak hegyesszögek függvényeiről tanultak. Ha nem szorítkozunk erre az esetre, akkor is tudjuk, hogy α és β közül legalább az egyik hegyesszög, ekkor (1) megfelelő oldala pozitív, tehát a másik is, s így a másik szögnek hegyesszögnek kell lennie.
2. A beküldött megoldások általában felhasználták a háromszögek színusz- vagy koszinusz-tételét ‐ amit még szintén nem tanultak az iskolában ‐, azonban a közölt megoldás mutatja, hogy egyszerűen célhoz érünk a koszinusz-függvény értelmezésén kívül csak I. osztályos ismereteket felhasználva is.
3. Továbbra is hegyesszögekre szorítkozva (1)-nek átrendezett
αcosβ=bcosα(2)
alakja alapján is megadhatjuk a választ a kérdésre, kizárólag a koszinusz-függvény definíciója alapján.
 
 
2. ábra
 

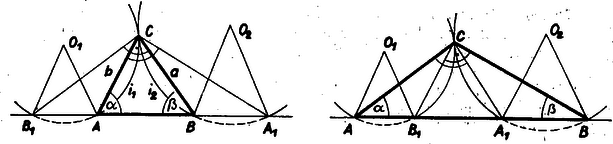Messe a C-ben CB-re, CA-ra állított merőleges AB-t B1-ben, ill. A1-ben. Így (2) azt teszi fel, hogy a BB1C és AA1C derékszögű háromszögek átfogója egyenlő (2. ábra):
BB1=AA1.(3)

Ez nyilvánvalóan teljesül, ha A1 azonos B-vel, vagyis ha C-nél derékszög van, hiszen ekkor B1 is azonos A-val.
γ<90∘ esetén A a BB1 szakaszon, B az AA1 szakaszon van, így (3)-ból AB-t levonva B1A=BA1, és ugyanez adódik γ>90∘ esetén is, ha AB=AB-ből (3)-at kivonjuk. A B1A és BA1 szakaszokat C-ből ugyanakkora szögben látjuk, ezért |γ-90∘| nyílású i1, i2 látóköríveik sugarai is egyenlők. Azokat az íveket véve, melyek AB-nek azon az oldalán vannak, mint C, az ív O1, ill. O2 középpontja a szakaszokkal egybevágó, egyenlő szárú háromszögeket alkot. A két ív egymás tükrös párja közös húregyenesükre, az ABC háromszög C-ből induló magasságvonalára nézve. Ugyanez áll tehát a CAB1, CBA1 háromszögpárra, vagyis az A, B pontpárra is, tehát ABC egyenlő szárú háromszög.
Ezek szerint a kérdéses háromszög vagy derékszögű, és benne a, b a befogók, vagy egyenlő szárú, és benne a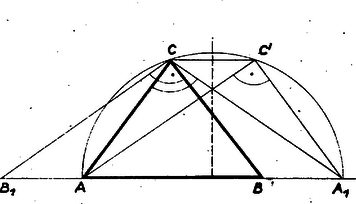, b a szárak.
 
 
3. ábra
 

4. A (3)-ra támaszkodva így is befejezhetjük a meggondolást (3. ábra): AA1C és BB1C egybevágó derékszögű háromszögek. Toljuk el az utóbbit úgy, hogy B1 az A-ba jusson, ekkor B az A1-be jut, ezért C-nek új, C' helyzete is rajta van az AA1 szakasz fölötti Thalész-körön. CC' felező merőlegese AA1-re is merőleges, ezen tükrözve AA1C' átmegy A1AC-be, tehát CA=C'A1=CB.