Kezdőlap


Feladat:	1105. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Balás Anna , Bálványos Zoltán , Baranyai Z. , Bauer Katalin , Bosznay Ádám , Hárs L. , Hárs László , Hernádi J. , Lengyel Erzsébet , Lengyel Tamás , Lőrincz András , Morvai István , Neszvada J. , Pataki János , Salamon G. , Schinagl Gábor , Schván Péter , Siklósi M. , Várhegyi Éva
Füzet:	1967/november, 150. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1967/január: 1105. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) A két kör kétféleképpen érintheti egymást. Külső érintkezés esetén a körök centrálisán $B$ , $A$ , $C$ a pontok sorrendje, és $D$ , $E$ a centrális két oldalán van, a konvex négyszög egymás utáni csúcsainak körüljárása $B D C E$ . Ezt a $B C$ átlóval két háromszögre vágva, ezek közös alapja a körök $d_{1}$ , $d_{2}$ átmérőjének összege, $m_{1}$ , ill. $m_{2}$ magasságuk pedig azonos az $A B D$ , ill. $A C E$ háromszög $B C$ -re merőleges magasságával. E két háromszög hasonló, mert $A$ -nál levő szögük egymás csúcsszöge, és $D$ -nél, ill. $E$ -nél Thalész tétele szerint derékszögük van. Így $m_{1} : m_{2} = d_{1} : d_{2}$ , $m_{2} = m_{1} d_{2} / d_{1}$ , és a kérdéses terület

\begin{matrix} t_{a} = (d_{1} + d_{2}) (\frac{m_{1}}{2} + \frac{m_{2}}{2}) = \frac{m_{1}}{2} \cdot (d_{1} + d_{2}) (1 + \frac{d_{2}}{d_{1}}) = m_{1} \cdot \frac{{(d_{1} + d_{2})}^{2}}{2 d_{1}} . \end{matrix}

B A D = α

szöget változtatva

t_{a}

kifejezésében csak az

m_{1}

tényező változik, így

t_{a}

akkor a legnagyobb, amikor

D

legtávolabb jut

B C

-től. Ekkor

D

az első kör

A B

-re merőleges átmérőjének végpontja,

A B D

egyenlő szárú derékszögű háromszög,

α = 45^{\circ}

m_{1} = d_{1} / 2

, és a terület legnagyobb értéke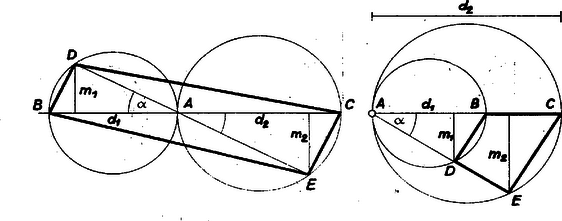

t_{a, max} = {(d_{1} + d_{2})}^{2} / 4

b) A körök belső érintkezése esetén

B

és

C

A

pontnak,

D

és

E

A B

egyenesnek ugyanazon oldalán van. Az a) esetben mondott hasonlóság itt is fennáll,

B D

és

C E

párhuzamosak, mert merőlegesek

A D

-re, és a konvex négyszög körüljárása

B C E D

. Területe egyenlő az

A C E

és

A B D

háromszögek területének különbségével (a jelölést úgy választottuk, hogy

d_{2} > d_{1}

\begin{matrix} t_{b} = \frac{d_{2} m_{2}}{2} - \frac{d_{1} m_{1}}{2} = \frac{d_{2}^{2} m_{1}}{2 d_{1}} - \frac{d_{1} m_{1}}{2} = m_{1} \cdot \frac{d_{2}^{2} - d_{1}^{2}}{2 d_{1}}, \end{matrix}

és ennek legnagyobb értéke az a) esethez hasonlóan

α = 45^{\circ}

m_{1} = d_{1} / 2

esetén következik be:

t_{b, max} = (d_{2}^{2} - d_{1}^{2}) / 4

Schinagl Gábor (Budapest, Képző- és Iparművészeti Gimn., II. o. t.)