| Feladat: | 1103. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Várhegyi Éva , Vitályos Gábor | ||
| Füzet: | 1968/január, 19 - 20. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Mértani helyek, Térgeometriai bizonyítások, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1967/január: 1103. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az négyzetlemez síkjától 5 cm-re levő pontok két vele párhuzamos, tőle 5 cm távolságra levő , síkon vannak. Ezeknek minden olyan pontja, amelynek -en levő vetülete belsejébe vagy a kerületére esik magától -től is 5 cm-re van, mert -nek -től különböző pontjaitól való távolsága nagyobb, mint 5 cm. Így e pontok hozzátartoznak a keresett mértani helyhez. A mondott pontok -en és -n kitöltik azt az -nel egybevágó , ill. négyzetet, melyek egymás utáni oldalegyeneseit az -re merőleges és rendre az -n, -n, -n, ill. -n átmenő sík metszi ki. Hasonlóan látjuk be, hogy és további pontjai 5 cm-nél nagyobb távolságra vannak -től. 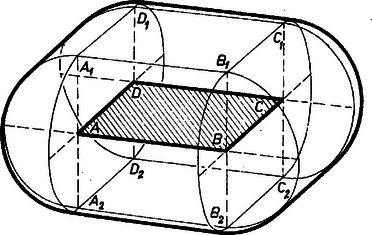 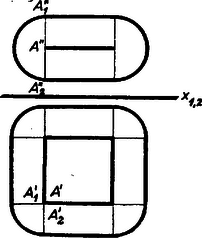 Az valamelyik oldalegyenesétől, mondjuk -től, 5 cm távolságra levő pontok azon a hengerpalást‐felületen vannak, melynek tengelye , sugara 5 cm. A palástnak minden olyan pontja, melynek -n levő vetülete az szakasz belsejébe vagy valamelyik végpontjába esik, és -en levő vetülete nincs az belsejében, magától -től is 5 cm-re van, hozzátartozik a mértani helyhez, mert -nek -től különböző pontjai 5 cm-nél távolabb vannak az ilyen -tól. (Ha az szakaszon adódik, akkor azonos -vel.) E pontok kitöltik a palástnak azt a darabját, amelynek határvonala egyrészt az és síkok által kimetszett félkör, másrészt az sík által kimetszett , alkotószakasz. A palást további pontjai -től vagy kisebb vagy nagyobb távolságra vannak, mint 5 cm. ‐ A , , szakaszokból egy‐egy a fentivel egybevágó fél‐hengerpalást adódik, mint a mértani hely része. Végül az valamelyik csúcsától, mondjuk -tól, 5 cm távolságra levő pontok az körül 5 cm sugárral írt gömb felületén vannak, közülük az a gömbkétszög alakú negyedrész tartozik a keresett mértani helyhez, mely a fenti és síknak -et nem tartalmazó partján van, vagy magán -n, -n. A gömbkétszög mindegyik határoló fél‐főköre egyszersmind a csatlakozó félhengerpalástnak alapköre. A , , csúcs ugyanígy egy‐egy negyedgömbbel járul hozzá a mértani helyhez. Összefoglalva: a mértani hely két négyzetlemezből, 4 fél‐hengerpalást felületből és 4 gömbkétszög alakú negyed‐gömbfelületből áll; a részek határvonalaikkal egymáshoz csatlakoznak és egy zárt, folytonos felületet alkotnak. A fentiekben a mértani helynek csupán az elképzelését tekintettük feladatunknak, a pontos meghatározáshoz hozzátartozó bizonyításokat viszont nem. Várhegyi Éva (Budapest, Berzsenyi D. g. I. o. t.) Megjegyzés. A mértani helyet elképzelhetjük úgy is, hogy egy 5 cm sugarú gömböt úgy mozgatunk minden lehetséges helyzetbe, hogy középpontja a lemez belsejében vagy oldalán vagy csúcsán legyen. Ekkor a súrolt pontok halmazának határfelülete, ún. konvex burka a mértani hely. Vitályos Gábor (Budapest, XII. ker., Mártonhegyi úti Ált. Isk., 8. o. t.) |