Kezdőlap


Feladat:	1095. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1967/december, 211 - 213. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Súlyvonal, Magasságvonal, Egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1966/december: 1095. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen az $A B C$ háromszög $A A_{1}$ , $B B_{1}$ súlyvonala mint átmérő fölé írt kör $k_{a}$ , ill. $k_{b}$ , középpontjuk $O_{a}$ , ill. $O_{b}$ (különbözők, hiszen felezik a súlyvonalat, azok közös pontja viszont harmadolja őket). A $C$ csúcsból akkor húzható a körökhöz érintő, ha $C$ -ben hegyesszög van. Ha ugyanis $A C B ∢ = 90^{\circ}$ , akkor $C$ mindkét körön rajta van, és ha $A C B ∢ > 90^{\circ}$ , akkor $C$ -t mindkét kör a belsejében tartalmazza.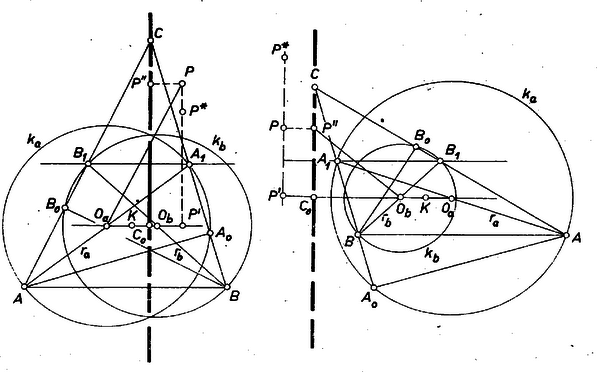
Ismeretes, hogy egy körhöz valamely külső pontból húzott érintőszakasz négyzete egyenlő a pontból induló bármely szelő két szeletének a szorzatával, így állításunkat megfelelő szelők felhasználásával bizonyítjuk be.

Legyen az

A C B ∢

hegyesszög és legyen

A

, ill.

B

vetülete a

C B

, ill.

C A

egyenesen

A_{0}

, ill.

B_{0}

, Ha

A_{0}

és

A_{1}

nem azonos, akkor

A_{0}

-ból az

A A_{1}

szakasz derékszög alatt látszik, tehát

A_{0}

rajta van

k_{a}

-n, így a

B C

egyenes

k_{a}

-t az

A_{0}

A_{1}

pontokban metszi. Ha pedig

A_{0}

és

A_{1}

azonos, akkor

A A_{1} ⊥ B C

, és

B C

érinti

k_{a}

-t. Mindkét esetben igaz tehát, hogy a

C

-ből

k_{a}

-hoz húzott érintőszakasz négyzete egyenlő a

C A_{1} \cdot C A_{0}

szorzattal. ‐ Hasonlóan kapjuk, hogy a

C

-ből

k_{b}

-hez húzott érintőszakasz négyzete egyenlő a

C B_{1} \cdot C B_{0}

szorzattal.
Az

A A_{0} C

B B_{0} C

háromszögek derékszögűek és hasonlók, hiszen

C

-beli szögük közös. Emiatt

\begin{matrix} C A : C A_{0} = C B : C B_{0}, \end{matrix}

tehát

C A_{0} \cdot C B = C A \cdot C B_{0}

, amiből

2

-vel való osztással kapjuk a bizonyítandó

C A_{0} \cdot C A_{1} = C B_{1} \cdot C B_{0}

egyenlőséget.

II. Mivel egy körhöz valamely külső pontból húzott

e

érintőszakasz merőleges az érintési ponthoz tartozó sugárra, az általuk meghatározott derékszögű háromszög alapján az érintőszakasz négyzete

d^{2} - r^{2}

-tel egyenlő ‐ ahol

r

a kör sugara, és

d

a külső pontnak a kör középpontjától mért távolsága.
Legyen a

k_{a}

k_{b}

körök sugara

r_{a}

r_{b}

, és egy tetszés szerinti ‐ mindkét körre nézve külső ‐

P

pontnak az

O_{a} O_{b}

egyenesen levő vetülete

P'

. Akkor a

P

-ből húzott érintőszakaszok négyzete

\begin{matrix} e_{a}^{2} = P P'^{2} + P' O_{a}^{2} - r_{a}^{2}, ill. e_{b}^{2} = P P'^{2} + P' O_{b}^{2} - r_{b}^{2} . \end{matrix}

P

-t a

P P'

egyenesen elmozdítjuk

P^{*}

-ba, akkor a fenti kifejezésekben csak a bennük közösen fellépő

P P'

szakasz hossza változik meg:

P^{*} P'

-re, így ha fennállt

e_{a} = e_{b}

, akkor

e_{a}^{*} = e_{b}^{*}

is teljesül, ahol

e_{a}^{*}

e_{b}^{*}

P^{*}

-ból húzott érintők hossza. Esetünkben tehát a

C

-n átmenő

O_{a} O_{b}

-re merőleges egyenesnek minden ‐ a körökre nézve külső ‐ pontjából a két körhöz húzott érintőszakaszok egyenlők.
Mivel pedig

O_{a}

is,

O_{b}

is egyenlő távol van az egymással párhuzamos

A B

A_{1} B_{1}

egyenesektől, s így

O_{a} O_{b} ∥ A B

, azért a

C

-ből

O_{a} O_{b}

-re bocsátott merőleges azonos az

A B C

háromszögnek

C

-ből húzott magasságegyenesével.
Megmutatjuk, hogy ‐ megfordítva ‐ ha a tetszés szerinti

P

pontból a

k_{a}

k_{b}

körökhöz húzott érintőszakaszok egyenlők, akkor

P

rajta van a

C

-hez tartozó magasságegyenesen. Legyen

C

vetülete az

O_{a} O_{b}

egyenesen

C_{0}

P

vetülete az

O_{a} O_{b}

és

C C_{0}

egyenesen

P'

, ill.

P''

, így azt kell belátnunk, hogy

P'

azonos

C_{0}

lal. A föltevés alapján, a fentiek felhasználásával

\begin{matrix} P P'^{2} + P' O_{a}^{2} - r_{a}^{2} = P P'^{2} + P' O_{b}^{2} - r_{b}^{2}, \end{matrix}

másrészt

P''

-re a fentiek szerint

\begin{matrix} P'' C_{0}^{2} + C_{0} O_{a}^{2} - r_{a}^{2} = P'' C_{0}^{2} + C_{0} O_{b}^{2} - r_{b}^{2} . \end{matrix}

Ezekből kivonással, átrendezéssel és a

P P' = P'' C_{0}

egyenlőségre tekintettel

\begin{matrix} P' O_{a}^{2} - P' O_{b}^{2} = C_{0} O_{a}^{2} - C_{0} O_{b}^{2} . \end{matrix}

(1)

Tegyük föl, hogy

B A C ∢ \leq A B C ∢ \leq 90^{\circ}

, amit ‐ ha kell ‐ az

A

B

betűk kezdeti fölcserélésével elérhetünk. Ekkor ‐ mint könnyen belátható ‐

C_{0}

O_{a} O_{b}

szakasz

K

felezőpontjának azon az oldalán van, mint

O_{b}

, vagy éppen

K

-ban,

C_{0} O_{a} \geq C_{0} O_{b}

, (1) jobb oldala nem negatív, így bal oldala sem, s emiatt

P' O_{a} \geq P' O_{b}

P'

ugyancsak a

K O_{b}

félegyenesen, vagy éppen

K

-ban van. Így

\begin{matrix} P' O_{a} & = K O_{a} + P' K, & P' O_{b} = | K O_{b} - P' K | = | K O_{a} - P' K |, \\ C_{0} O_{a} & = K O_{a} + C_{0} K, & C_{0} O_{b} = | K O_{a} - C_{0} K |, \end{matrix}

ezeket (1)-be helyettesítve

P' K = C_{0} K

, ami állításunkat igazolja.

Összefoglalva a fentieket, kimondhatjuk, hogy egy külső

P

pontból a

k_{a}

k_{b}

körökhöz húzott érintőszakaszok akkor és csak akkor egyenlők, ha

P

A B C

háromszög

C

csúcsához tartozó magasságvonalán van.

Több dolgozatból, kiegészítésekkel

Megjegyzés. Egy adott körhöz és egy tetszőleges ponthoz tartozó

d^{2} - r^{2}

kifejezés értékét az illető pontnak az adott körre vonatkozó hatványának nevezzük. A megoldás második felében végzett meggondolások akkor is érvényesek, ha a

d^{2} - r^{2}

kifejezés értéke

0

vagy negatív. Természetesen ebben az esetben a pont nem külső pontja a körnek, így nem beszélhetünk érintőről; az viszont, hogy a

d^{2} - r^{2}

kifejezés értéke egyenlő a ponton átmenő szelő szeleteinek a szorzatával, ebben az esetben is igaz, ha a belső ponton átmenő szelő szeleteit ellentétes előjelűnek tekintjük. Megállapításunkat tehát így is kimondhatjuk: azoknak a pontoknak a mértani helye, melyeknek két adott körre vonatkozó hatványa egyenlő, egy a körök centrálisára merőleges egyenes, szokásos nevén a két kör hatványvonala. Ez az egyenes nyilván átmegy a körök közös pontján ‐ ha van közös pontjuk ‐, mert a közös pont hatványa mindkét körre nézve

0

, vagyis azonos a körök közös húregyenesével, érintkezés esetén közös érintőjükkel. Ha nincs közös pont, akkor a hatványvonal egyik kört sem metszi.