Feladat: 1079. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Backhausz Beáta ,  Bálványos Z. ,  Bense Magdolna ,  Csóka Erzsébet ,  Fiala T. ,  Hárs László ,  Kóczy L. ,  Komjáth P. ,  László I. ,  Lempert L. ,  Maróti P. ,  Papp Zoltán ,  Pataki I. ,  Pataki János ,  Somogyi Á. ,  Süttő Judit ,  Süttő Klára ,  Varga Katalin ,  Zambó Péter 
Füzet: 1967/október, 63 - 66. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Egyenlőtlenségek grafikus megoldása, Kör (és részhalmaza), mint mértani hely, Diszkusszió, Háromszögek szerkesztése, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):Feladatok: 1966/október: 1079. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Legyen az előírásoknak megfelelő ABC háromszög BC oldalszakaszának első és harmadik negyedelő pontja D, ill. E(DC=3BD, BE=3EC), és AB, AD, AE rendre egyenlő az adott c, d, ill. e szakasszal (1. ábra). Húzzunk párhuzamost D-n át AE-vel, és messe ez AB-t F-ben. D harmadolja BE-t, így F is harmadolja BA-t, ezért egyrészt AF=2c/3, másrészt FD=AE/3=e/3, így az AFD háromszög oldalai megszerkeszthetők az adott szakaszokból.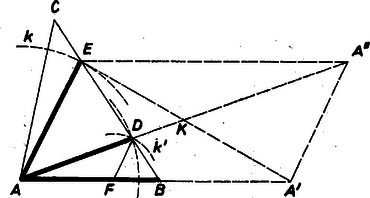
 
 
1. ábra
 

E háromszöget előállítva, az A-ból induló, FD-vel párhuzamosan húzott félegyenesre fölmérjük e-t, ekkor DE és AF metszéspontja megadja B-t, végül BD-t fölmérve BE-nek E-n túli meghosszabbítására, kapjuk C-t.
A szerkesztés szerint egyrészt AE=3FD miatt AB=3⋅FB=FB+2c/3, és így FB=c/3, AB=c, másrészt ugyanígy BE=3⋅BD, ennélfogva BC=4BD, végül AD=d, AE=e, tehát az ABC háromszög megfelel a követelményeknek.
Az AFD háromszög létrejön, ha
|2c3-e3|<d<2c3+e3,azaz ha|2c-e|<3d<2c+e.(1)
E feltétel teljesülése esetén 1 háromszöget kapunk.
b) Legyen a három szakasz először 6, 4 és 1 egységnyi. Közülük c-t 3-féleképpen választhatjuk meg, d-t mindegyik esetben a maradó szakaszok közül 2-féleképpen, e pedig mindig a nem választott szakasz lesz, tehát a következő 3⋅2=6 szereposztást kell megvizsgálnunk:
c,d,e=6,4,1;6,1,4;4,6,1;4,1,6;1,6,4;1,4,6.
(1) csak az első és a negyedik esetben teljesül, ebből a szakaszhármasból 2 megoldást kapunk.
Hasonlóan a 9, 6, 5 szakaszhármasból 4 megoldást kapunk, csak a c, d, e=6, 9, 5 és 5, 9, 6 szereposztásokban nem teljesül (1), vagyis amikor d-t próbáljuk legnagyobbnak. Valóban, az ADB és ADE háromszögek egyike D-nél tompaszögű, vagy mindkettő derékszögű, ezért AD az AB és AE szakaszok közül legalább az egyiknél kisebb. Eszerint 4-nél több megoldást sohasem kaphatunk.
 
Süttő Judit (Budapest, Ságvári E. gyak. g. I. o. t.)
Hárs László (Budapest, Kölcsey F. g. II. o. t.)
Pataki János (Budapest, Berzsenyi D. g. I. o. t.)
 

Megjegyzések. 1. A 2c, 3d, e oldalú háromszög megszerkesztésére jutunk pl. a következő gondolatmenettel: A tükörképét B-re A'-vel jelölve az AA'E háromszögben EB súlyvonal, D súlypont, így AD és A'E metszéspontját K-val, A tükörképét K-ra A''-vel jelölve AK, mint súlyvonal (3/2) AD hosszúságú, ezért AA''=2AK=3AD, és az AA'A''E paralelogrammából A'A''=AE=e, tehát az AA'A'' háromszög szerkeszthető a 2c, 3d, e oldalakból.
2. A fenti megoldásra elvezet a következő elemzés is. Felvéve az AB=c szakaszt, E az A körüli e sugarú k körön lesz. Mivel D a BE szakasz B-hez közelebbi harmadoló pontja, azért D-nek egy mértani helyét kapjuk, ha k-t B-ből mint középpontból harmadára zsugorítjuk, legyen ez k'. D másik mértani helye az A körüli d sugarú kör. ‐ Az így kapott BD szakaszt B-ből 3-, ill. 4-szeresére nyújtva kapjuk E-t, ill. C-t.
 Papp Zoltán (Debrecen, Fazekas M. g. II. o. t.)
 

II. megoldás az a) részre (vázlat). Tovább használjuk a fenti A, B, C, D, E jelöléseket. A keresetthez hasonló A*B*C* háromszöget szerkesztünk, felhasználva Apollóniosz tételét 1 ‐ mely szerint a sík azon pontjainak mértani helye, amelyek két adott ponttól mért távolságainak aránya állandó (és 1-től különböző), kör ‐, azután ezt a kívánt nagyságúra transzformáljuk. Legyen a tetszés szerinti B*C* szakasz első és harmadik negyedelő pontja D*, ill. E*, ekkor a kívánt hasonlóság miatt
A*B*:A*D*=AB:AD=c:d,A*B*:A*E*=c:e,
tehát A* annak a két Apollóniosz-körnek, k1-nek és k2-nek a metszéspontja, melyek alappontjai és aránymutatója
(k1):B*,D*,c:d(≠1),ill.(k2):B*,E*,c:e(≠1),
(ugyanis a feltevés szerint d≠c≠e).
Nyilvánvaló, hogy a két körnek a B*C*=a* egyenes szimmetriatengelye, ezért a*-nak az az X, Y pontpárja, amelyre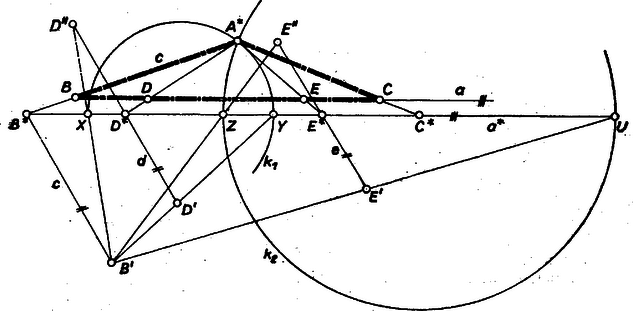
XB*:XD*=YB*:YD*=c:d
(X a B*D* szakasz belsejében, Y pedig kívül rajta), k1-nek egy átmérőjét adja meg, és ezzel maga k1 is meg van határozva. A szerkesztés (2. ábra):
 
 
2. ábra
 

Egy a* egyenes egymás utáni B*, D*, E*, C* pontját úgy vesszük fel, hogy B*D*=E*C* és D*E*=2B*D*. Az első három ponton át egymással párhuzamos egyeneseket veszünk fel, majd rendre felmérjük rájuk a
B*B'=c,D*D'=D*D''=d,E*E'=E*E''=e
szakaszokat (B', D', E' az a* egyik partján, D'', E'' a másikon; mérhetünk természetesen tc, td, te szakaszt, ahol t>0, tetszés szerinti szám). Ekkor a fenti X-et a B'D'', Y-t a B'D' egyenes metszi ki a*-ból, k2 megfelelő átmérőjének Z, U végpontjait pedig hasonlóan B'E'', B'E'. k1 és k2 egyik metszéspontjából, A*-ból kiindulva félegyeneseket húzunk B*-on és C*-on át, az előbbire felmérjük az A*B=c szakaszt, B-n át meghúzzuk az a*-gal párhuzamos a egyenest. Ekkor a és A*C* metszéspontját C-vel jelölve az A*BC háromszög megfelel a követelményeknek. ‐ Ennek bizonyítását helyszűke miatt az olvasóra hagyjuk, valamint annak vizsgálatát is, mely feltételek esetén van k1-nek és k2-nek a*-on kívül A* közös pontja, vagyis a feladatnak megoldása.
 
 Bense Magdolna (Kiskunfélegyháza, Móra F. g. II. o. t.)
1Lásd pl. Gallai T.‐Hódi E.‐Péter R.‐Szabó P.‐Tolnai J.: Matematika a gimn. III. o. számára, 12. kiadás, Tankönyvkiadó, Bpest 1962., 177. o.