Kezdőlap


Feladat:	1071. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Bajmóczy Ervin , Fiala Tibor
Füzet:	1967/április, 166 - 168. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Középpontos tükrözés, Eltolás, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1966/szeptember: 1071. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A leírt helyzet létrejön pl. az 1. ábra szerint, úgy, hogy a $C A$ , $C_{1} A_{1}$ oldalpáron haladva egyirányban mozgunk, $A B$ -n és $A_{1} B_{1}$ -en pedig ellentétes irányban; így $A$ -ban balra, $A_{1}$ -ben pedig jobbra fordulunk el előző menetirányunkhoz képest. Legyen $A_{1}$ , $B_{1}$ , $C_{1}$ tükörképe rendre az $A$ , $B$ , ill. $C$ középpontra nézve $A_{2}$ , $B_{2}$ , $C_{2}$ , a velük meghatározott háromszög 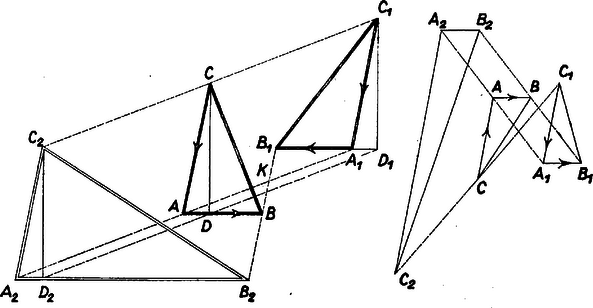$H_{2}$ .

\begin{matrix} 1. és 2. ábra \end{matrix}

C A # C_{1} A_{1}

feltevés miatt

C A A_{1} C_{1}

paralelogramma, tehát

C C_{1}

és

A A_{1}

egyirányúan párhuzamosak és egyenlők, ezért ugyanez áll a tükrözésükkel előálló

C C_{2}

A A_{2}

szakaszokra, tehát

C C_{2} A_{2} A

paralelogramma, és így

C_{2} A_{2}

párhuzamos, egyirányú és egyenlő

C A

-val és

C_{1} A_{1}

-gyel.

A B # A_{1} B_{1}

miatt

A B A_{1} B_{1}

paralelogramma, átlói

A A_{1}

és

B B_{1}

, legyen metszéspontjuk

K

. Így

K A = A A_{1} / 2

K A_{2} = 3 \cdot A A_{1} / 2

, továbbá

B B_{2} = B B_{1}

és

K B = B B_{1} / 2

miatt

K B_{2} = 3 \cdot B B_{1} / 2

, és

A_{2}

K A

félegyenesen,

B_{2}

K B

-n van. Eszerint a

K A_{2} B_{2}

és

K A B

háromszögek hasonló helyzetűek a

K

középpontra nézve, a nagyítás aránya

3 : 1

, tehát

A_{2} B_{2} ∥ A B ∥ A_{1} B_{1}

, és

A_{2} B_{2} = 3 \cdot A B

.
Így a

H

H_{1}

H_{2}

háromszögben a,

C D

C_{1} D_{1}

, ill.

C_{2} D_{2}

magasságok is párhuzamosak, ezért az

A C D

A_{1} C_{1} D_{1}

A_{2} C_{2} D_{2}

szögek, mint egyállású szögek, egyenlők, az ezeket tartalmazó derékszögű háromszögek az átfogók már belátott egyenlősége miatt egybevágók, tehát

C D = C_{1} D_{1} = C_{2} D_{2}

. (Amennyiben

C A

merőleges

A B

-re, akkor

D

D_{1}

D_{2}

rendre azonos az

A

A_{1}

A_{2}

csúccsal.)
Mindezek szerint, a területet is az illető háromszög jelével jelölve

\begin{matrix} H = \frac{1}{2} A B \cdot C D = \frac{1}{2} \cdot A_{1} B_{1} \cdot C_{1} D_{1} & = H_{1}, és H_{2} = \frac{1}{2} A_{2} B_{2} \cdot C_{2} D_{2} = \frac{1}{2} \cdot 3 A B \cdot C D = \\ = 3 H = 3 H_{1} . \end{matrix}

Ezt kellett bizonyítanunk.
A feladatban leírt helyzet még egy módon létrejöhet. Ha

H

és

H_{1}

előírt körüljárásában az

A B

A_{1} B_{1}

oldalpáron haladva ugyanabban az irányban mozgunk, akkor az ellentétes irányú körüljárás csak úgy adódhatott, ha az előző

C A

C_{1} A_{1}

oldalpáron ellentétes irányban mozogtunk (2. ábra). Ebből a helyzetből a

B

C

, valamint

B_{1}

C_{1}

betűpárok fölcserélésével a fentit kapjuk, és az új betűzés szerinti körüljárások is egymással ellentétes irányúak, mert az új irány mindkét háromszögben ellentétes irányú az eredetivel.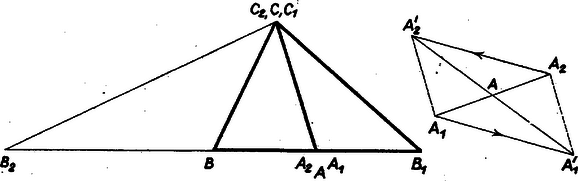

Fiala Tibor (Budapest, Rákóczi F. g. II. o. t.)

II. megoldás. Egyszerű helyzet adódik, ha

A_{1}

egybeesik

A

-val és

C_{1}

C

-vel (3. ábra), hiszen két egyenes egybeesése a párhuzamosság különleges esete; más szóval ugyanaz az egyenes játssza

A C

és

A_{1} C_{1}

szerepét. Ebben a helyzetben ugyanis

A_{2}

A

-ba esik,

C_{2}

C

-be, továbbá

B

és

B_{1}

egymás tükörképei

A

-ra,

B_{2}

is az

A B

egyenesen adódik, vagyis mindhárom háromszögnek egy oldala ‐

A B

A_{1} B_{1}

, ill.

A_{2} B_{2}

‐ ugyanazon az egyenesen van. Továbbá közös az erre merőleges magasságuk is, és a bizonyítás leszűkül

A_{2} B_{2} = 3 A B

belátására:

A

felezi

B B_{1}

-et,

B

felezi

B_{2} B_{1}

-et, tehát

A_{2} B_{2} = A B_{2} = A B + B B_{2} = A B + B B_{1} = A B + 2 A B = 3 A B

\begin{matrix} 3. és 4. ábra \end{matrix}

Eszerint elég azt belátnunk, hogy ha

H_{1}

-et valamilyen irányban eltoljuk a

H'_{1} = A'_{1} B'_{1} C'_{1}

helyzetbe, és a vesszős csúcsok tükörképe a megfelelő

A

B

C

középpontra nézve rendre

A'_{2}

B'_{2}

C'_{2}

, akkor az ezekkel meghatározott

H'_{2}

háromszög

H_{2}

-nek eltolt képe, tehát egybevágó vele, területük egyenlő. Pontosabban azt állítjuk, hogy

H'_{2}

-t a

H_{2}

-be a fentivel ellentétes irányú, egyenlő nagyságú eltolás viszi át. Ezt is elég egyetlen csúcsra belátni, ez pedig abból látható, hogy a szerkesztés szerint az

A_{2} A'_{2}

elmozdulás az

A_{1} A'_{1}

elmozdulás tükörképe

A

-ra nézve (4. ábra), más szóval

A

körüli

180^{\circ}

-os elforgatottja. Az irány e forgatás miatt válik ellentétessé.
Ezek szerint az 1. ábra

H_{1}

háromszögét úgy eltolva, hogy

A_{1}

A

-ba jusson,

C_{1}

C

-be jut, és a területek megváltozása nélkül előáll a vizsgált egyszerű helyzet.

Bajmóczy Ervin (Budapest, Ady E. Ált. Isk. (és G.) 8. o. t.)