Kezdőlap


Feladat:	1064. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Backhausz Beáta , Bajmóczy Ervin , Bálványos Z. , Csirmaz László , Dobozy O. , Dőry Anna , Eszes G. , Fiala T. , Gegesy F. , Hárs László , Herneczki I. , Horváth László , Horváth Sándor , Juhász Ágnes , Juhász Judit , Katona Viktor , Kóczy L. , Lampert L. , Móricz P. , Moson Péter , Nikodémusz Anna , Orbán G. , Pataki I. , Perémy Gábor , Pintér Ágnes , Pintz János , Siklósi M. , Somos E. , Stefanovicz K. , Szabados Katalin , Szalay Marianne , Szűcs A. , Takács László , Tátray P. , Vályi I. , Várhelyi F. , Vetiner A.
Füzet:	1967/március, 117 - 119. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Logikai feladatok, Egyéb sokszögek geometriája, Ellenpélda, mint megoldási módszer a matematikában, Gyakorlat
Hivatkozás(ok):	Feladatok: 1966/május: 1064. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az I. állítás igaz. Ugyanis a kör középpontját a sokszög csúcsaival összekötve egybevágó egyenlő szárú háromszögeket kapunk, és a sokszög mindegyik szöge $2$ -szer akkora, mint e háromszögekben az alapon fekvő szög. (Az $n = 3$ esetben az állítás helyes volta egyszerűbben adódik a kör felhasználása nélkül, hiszen minden háromszög körbeírt.)
A II. állítás hamis. $n = 4$ esetén a rombusz megfelel a feltételeknek ‐ beírt körének középpontja az átlók metszéspontja ‐, de szögei általában nem egyenlők.
A III. állítás szerint ha egy körbeírt $n$ -szög szögei egyenlők, akkor oldalai is egyenlők. Ez hamis, $n = 4$ esetén a téglalap megfelel a feltételeknek, de oldalai általában nem egyenlők.
A IV. állítás ezt mondja ki: ha egy kör köré írt $n$ -szög szögei egyenlők, akkor oldalai is egyenlők. Ez igaz. Az $n$ -szög bármely két szomszédos oldalának érintési pontjához húzott sugarak szöge ugyanakkora, az $n$ -szög szögének kiegészítő szöge. Ezért bármely két ilyen sugárpár által meghatározott egyenlő szárú háromszög egybevágó, harmadik oldaluk az $n$ -szög két szomszédos oldala érintési pontjának távolsága, mindig ugyanakkora. Ez az oldal az $n$ -szög figyelembe vett két oldalának a közös csúcstól az érintési pontig terjedő szakaszával egyenlő szárú háromszöget alkot, mert, a körhöz külső pontból húzott érintőszakaszok egyenlők. Bármely két ilyen háromszög egybevágó, mert alapjuk és a szárak közti szögük egyenlő. Ezért az $n$ -szög bármely két csúcsából húzott érintőszakaszok egyenlők. Így az $n$ -szög oldalai is egyenlők, mert $2$ ‐ $2$ érintőszakaszból tevődnek össze. ( $n = 3$ esetén ez az állítás is egyszerűbben adódik a kör felhasználása nélkül.)
Az V. és a VI. állítás az I-nek speciális esete $n = 5$ , ill. $n = 6$ esetére, tehát helyes, ugyanígy a XI. és a XII. állítás is, mint a IV-nek speciális esetei.

1. ábra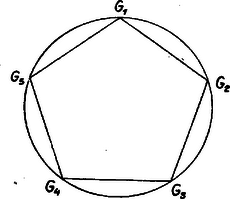

2. ábra

Megmutatjuk még, hogy a

C_{5}

-re és

B_{5}

-re vonatkozó VII., ill. IX. állítás helyes, a

C_{6}

-ra és

B_{6}

-ra vonatkozó VIII., ill. X. állításra viszont ellenpéldát adunk, ezek általában nem igazak.
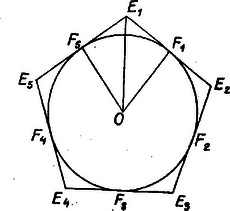
A VII. állítás így is kimondható: az egyenlő oldalú

E_{1} E_{2} E_{3} E_{4} E_{5} =

Ö érintő ötszög szögei egyenlők. Érintse a beírt kör Ö-nek egymás utáni oldalait rendre

F_{1} -ben,...,F_{5} -ben

(1. ábra), és legyen a kör középpontja

O

. Ekkor a külső pontból húzott érintők egyenlő volta miatt

\begin{matrix} F_{5} E_{1} = E_{1} F_{1} = E_{1} E_{2} - F_{1} E_{2} = E_{2} E_{3} - F_{2} E_{2} = F_{2} E_{3}, \end{matrix}

azaz Ö kerületét a csúcsok fenti sorrendjében bejárva egy oldalnak az érintési pont és a végpont közti szakasza egyenlő a

2

-vel utána következő (valamint a

2

-vel előtte levő) oldal megfelelő szakaszával. Továbbmenve

\begin{matrix} F_{2} E_{3} = F_{4} E_{5} = E_{5} F_{5}, tehát F_{5} E_{1} = E_{5} F_{5}, \end{matrix}

F_{5}

felezi a rajta átmenő

E_{5} E_{1}

oldalt, és ugyanez áll a további érintési pontokra is. Megrajzolva az

O E_{i}

és

O F_{i}

szakaszokat

(i = 1, 2, 3, 4, 5)

, mind a

10

keletkező derékszögű háromszög befogói egyenlők, a háromszögek egybevágók, és Ö mindegyik csúcsánál

2

-szer akkora szög van, mint e háromszögeknek az

O F_{i}

befogóval szemben levő szöge. Ezzel az állítást igazoltuk.
A IX. állítás: az egyenlő szögű

G_{1} G_{2} G_{3} G_{4} G_{5}

húrötszög oldalai egyenlők (2. ábra). Valóban

G_{5} G_{1} G_{2} ∢ = G_{1} G_{2} G_{3} ∢

miatt a száraik között levő

G_{5} G_{4} G_{2}

és

G_{1} G_{5} G_{3}

ívek egyenlők. Ezért az ezeket teljes körré kiegészítő

G_{5} G_{1} G_{2}

és

G_{1} G_{2} G_{3}

ívek, valamint a közös

G_{1} G_{2}

részük elhagyásával adódó

G_{5} G_{1}

és

G_{2} G_{3}

ívek is, ennélfogva a

G_{5} G_{1}

és

G_{2} G_{3}

húrok is egyenlők. Más szóval, az ötszög mindegyik oldala egyenlő a rá következő második oldallal:

\begin{matrix} G_{5} G_{1} = G_{2} G_{3} = G_{4} G_{5} = G_{1} G_{2} = G_{3} G_{4}, \end{matrix}

tehát mind az

5

oldal egyenlő. Ezt akartuk bizonyítani.
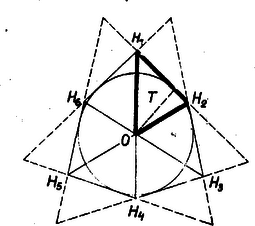
A VIII. állításra térve legyen az

O H_{1} H_{2} = T

háromszög

O

-nál levő szöge

60^{\circ}

, további két szöge egymástól különböző hegyesszög, és forgassuk el

T

-t

O

körül, mindkét irányban

120^{\circ}

-kal az

O H_{3} H_{4}

ill.

O H_{5} H_{6}

helyzetbe (3. ábra). Ekkor az

O H_{3} H_{2}

O H_{5} H_{4}

O H_{1} H_{6}

háromszögek (tükrösen) egybevágók

T

-vel, mert pl.

O H_{3} = O H_{1}

és

H_{2} O H_{3} ∢ = 120^{\circ} - 60^{\circ} = 60^{\circ} .

Ezért a

H_{1} H_{2} H_{3} H_{4} H_{5} H_{6}

hatszög oldalai egyenlők, és érintik azt az

O

körüli kört, melynek sugara

T

-nek

O

-ból kiinduló magassága, tehát teljesítik a

C_{6}

feltételt. Ellenben a hatszög bármelyik két szomszédos szöge különböző, mert

2

-szer akkora, mint

T

-nek

H_{1}

-nél, ill.

H_{2}

-nél levő szöge. (Csak minden második szög egyenlő.) Hatszögünk úgy is előállítható, hogy egy szabályos háromszöget a középpontja körül

60^{\circ}

-nál kisebb, tetszés szerinti szöggel elforgatunk és vesszük az eredeti és az új háromszög közös részét.

3. ábra

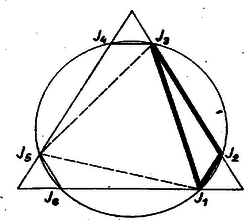
Végül a X. állításra a következő szerkesztés ad ellenpéldát. Vegyünk egy szabályos háromszöget, és mérjünk fel mindegyik csúcsából a másik két csúcs felé ugyanakkora, az oldal harmadánál kisebb szakaszt (4. ábra). Nyilvánvaló, hogy a

6

végpont által meghatározott konvex hatszög körbe írható és hogy szögei egyenlők, oldalai viszont különbözők. (Csak minden második oldal egyenlő.) ‐ Ezzel állításainkat bebizonyítottuk.
Utóbbi ellenpéldánkat a VIII. állítás ellenpéldájához hasonlóan is származtathatjuk: legyen a

J_{1} J_{2} J_{3} = U

háromszögben a

J_{2}

-nél levő szög

120^{\circ}

és

J_{1} J_{2} < J_{2} J_{3}

, és forgassuk el

U

-t a köréje írt kör középpontja körül mindkét irányban

120^{\circ}

-kal.

4. ábra

A VII. és IX. állítások bizonyításában közös elem volt, hogy egy-egy tulajdonság átöröklődött az ötszög valamelyik oldaláról a rá következő második oldalra és hogy

2

‐

2

oldallal előre haladva az idom kerületén, az ötszöget

2

-szer körüljárhattuk, az első körüljárásban kimaradt oldalakra is átöröklődhetett a tulajdonság. A VIII. és X. állítások esetében viszont ‐ a hatszögben ‐

2

‐

2

oldallal előre lépve

3

lépés után visszajutunk a kiindulási oldalhoz, a kihagyott oldalakra később sem juthatunk el, a tulajdonság azokra nem öröklődhet át, ill. azokon más tulajdonság öröklődik. Ebből látjuk, hogy

5

helyére nagyobb páratlan számot írva VII. és IX. megfelelője:

C_{2 n + 1}

, akkor

P

: igaz állítás, illetőleg
ha

B_{2 n + 1}

, akkor

Q

: igaz állítás;
viszont VIII. és X. megfelelője:
ha

C_{2 n}

, akkor

P

: hamis állítás; illetőleg
ha

B_{2 n}

, akkor

Q

: hamis állítás.

Takács László (Sopron, Széchenyi I. Gimn., II. o. t.)