Kezdőlap


Feladat:	1040. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Scherer Ferenc
Füzet:	1966/november, 152 - 153. oldal		PDF \| MathML
Témakör(ök):	Négyszög alapú egyéb hasábok, Paralelogrammák, Gyakorlat, Pitagorasz-tétel alkalmazásai
Hivatkozás(ok):	Feladatok: 1966/február: 1040. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Derékszögű paralelogrammában az állítás érvényessége nyilvánvaló. Legyen az $A B C D$ paralelogrammában $A B \geq A D$ és $B A D ∢ < A B C ∢$ . Ekkor az $A B$ egyenest a rá $D$ -ből bocsátott magasság $A$ és $B$ között metszi egy $D'$ pontban, a $C$ -ből húzott magasság pedig a $B$ -n túli $C'$ -ben. Így az $A C C'$ és $B D D'$ derékszögű háromszögekből Pitagorasz tétele alapján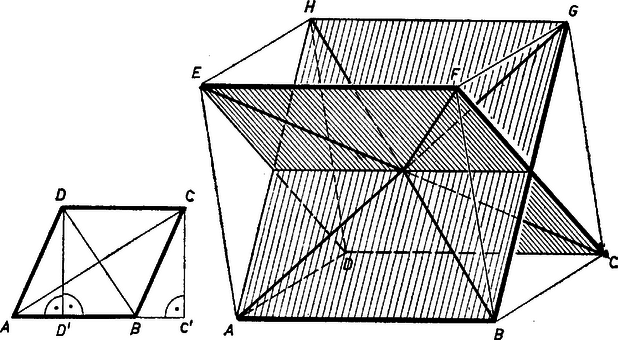

\begin{matrix} A C^{2} = {(A B + B C')}^{2} + C C'^{2} = A B^{2} + 2 A B \cdot B C' + (B C'^{2} + C C'^{2}), \\ B D^{2} = {(A B - A D')}^{2} + D D'^{2} = A B^{2} - 2 A B \cdot A D' + (A D'^{2} + D D'^{2}), \end{matrix}

ezek összegéből pedig, figyelembe véve az

A B = C D

A D' = B C'

egyenlőségeket, valamint hogy a zárójelekben a

B C C'

és

A D D'

derékszögű háromszögek befogóinak négyzetösszege áll:

\begin{matrix} A C^{2} + B D^{2} = A B^{2} + C D^{2} + B C^{2} + A D^{2} . \end{matrix}

Ezt kellett bizonyítanunk.

b) Legyen a hasáb alapja az

A B C D

, fedőlapja az

E F G H

paralelogramma úgy, hogy az oldalélek

A E

B F

C G

D H

. A hasáb oldallapjai is paralelogrammák, így

A B # C D # G H # F E

. Ezért az

A B G H

és

C D E F

négyszögek is paralelogrammák, és a hasáb

A G

B H

C E

D F

testátlói e két paralelogramma átlói. A bizonyítandó állítást úgy kapjuk, hogy az a) részben bebizonyított tételt alkalmazzuk az

A B G H

C D E F

B C G F

A D H E

paralelogrammákra, az egyenlőségeket összeadjuk és a két oldalon fellépő azonos tagokat ‐ az utóbbi két paralelogramma átlóinak négyzetét ‐ elhagyjuk:

\begin{matrix} A G^{2} + B H^{2} = A B^{2} + G H^{2} + B G^{2} + A H^{2}, \\ C E^{2} + D F^{2} = C D^{2} + E F^{2} + C F^{2} + D E^{2}, \\ B G^{2} + C F^{2} = B C^{2} + F G^{2} + B F^{2} + C G^{2}, \\ A H^{2} + D E^{2} = A D^{2} + E H^{2} + A E^{2} + D H^{2}. \\ A G^{2} + B H^{2} + C E^{2} + D F^{2} = \\ = (A B^{2} + C D^{2} + G H^{2} + E F^{2}) + (A D^{2} + B C^{2} + F G^{2} + E H^{2}) + \\ + (A E^{2} + B F^{2} + C G^{2} + D H^{2}). \end{matrix}

Scherer Ferenc (Esztergom, Temesvári Pelbárt g. II. o. t.)