Kezdőlap


Feladat:	1038. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berács József , Dőry Anna , Hárs L. , Herczog L. , Kovács Tamás , Mérő L. , Mészáros J. (Makó) , Mitrocsák Anikó , Moson P. , Orbán G. , Pap Márta , Perémy G. , Pintér Ágnes , Pintz J. , Somos E. , Szentmiklósi L. , Szücs A. , Takács L. , Vályi I. , Várhelyi F.
Füzet:	1966/november, 151 - 152. oldal		PDF \| MathML
Témakör(ök):	Forgatva nyújtás, Háromszögek nevezetes tételei, Kombinatorikus geometria síkban, Gyakorlat
Hivatkozás(ok):	Feladatok: 1966/február: 1038. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Válasszuk az adott háromszög betűzését úgy, hogy csúcsait $A$ , $B$ , $C$ sorrendben körüljárva a háromszög belseje az útvonaltól balra legyen, más szóval $A B C$ pozitív körüljárást adjon. Legyenek az oldalakra befelé írt háromszögek $A B C_{1}$ , $B C A_{1}$ , $C A B_{1}$ , a kifelé írtak $B A C_{2}$ , $C B A_{2}$ , $A C B_{2}$ (1. a ‐ 1. b ábrák). A feltevés szerint az $A C_{1} B_{2}$ , $C_{2} B A_{1}$ , $B_{1} A_{2} C$ háromszögek úgy keletkeznek az $A B C$ háromszögből, hogy ezt rendre az $A$ , $B$ , $C$ pont körül a pozitív forgási irányban $60^{\circ}$ -kal elfordítjuk, ezért az $A B$ , $B C$ , $C A$ oldalak új helyzetei hármasával egyenlő és párhuzamos szakaszokat adnak:

\begin{matrix} A C_{1} # C_{2} B # B_{1} A_{2}, C_{1} B_{2} # B A_{1} # A_{2} C, B_{2} A # A_{1} C_{2} # C B_{1} . \end{matrix}

(1)

1.a. és 1.b. ábra

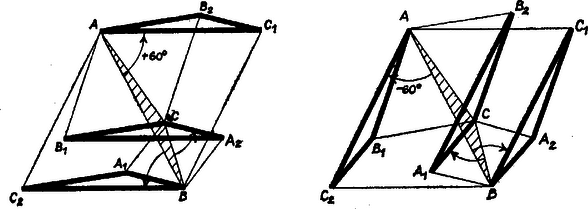Bármelyik szakaszhármas két szakasza egy paralelogramma két szemben fekvő oldalát adja. Egy hármasból két szakaszt

3

-féleképpen választhatunk ki ‐ ti. azzal, hogy egymás után mindegyiket egyszer nem választjuk bele a szakaszpárba, így a

3

hármasból

3 \cdot 3 = 9

féleképpen kaphatjuk egy-egy paralelogramma csúcsait.
Hasonlóan az

A C_{2} B_{1}

C_{1} B A_{2}

B_{2} A_{1} C

háromszögek az

A B C

háromszögnek

A

, majd

B

, végül

C

körüli, negatív irányú

60^{\circ}

-os elfordítottjai, ezért az

\begin{matrix} A C_{2}, C_{1} B, B_{2} A_{1}; C_{2} B_{1}, B A_{2}, A_{1} C; B_{1} A, A_{2} C_{1}, C B_{2} \end{matrix}

(2)

szakaszhármasok bármelyik párja is paralelogrammát ad, de ezek azonosak a fentiekkel, most mindegyiküket az előbb nem említett oldalpárjuk révén kaptuk meg.
Amennyiben az

A B C

háromszögben van

60^{\circ}

-os vagy

120^{\circ}

-os szög, egy-egy szakaszpár egy egyenesre esik, egy-egy paralelogramma elfajul egyenesszakasszá.
II. Az oldalak fölé egyenlő szárú derékszögű háromszögeket rajzolva minden ilyen háromszögben a szárak ‐ vagyis a befogók ‐

\sqrt[]{2}

-ször kisebbek az átfogónál, az eredeti háromszög megfelelő oldalánál, másrészt az átfogón levő szögek mindegyike

45^{\circ}

. Eszerint ‐ ismét a fenti betűzést használva ‐ a fenti két háromszög-hármas mindegyik tagja forgatva nyújtással keletkezik az eredeti háromszögből, a forgatás szöge

45^{\circ}

, iránya a két háromszög-hármasban megegyező, a nyújtás aránya

1 / \sqrt[]{2}

, ezért az (1) és (2) szakaszhármasok tagjai között ismét fennáll az egyenlőség és a párhuzamosság, az állítás érvényes marad (2. ábra).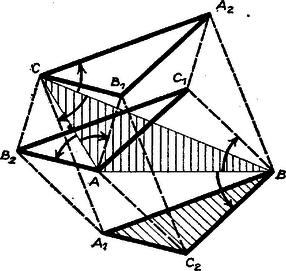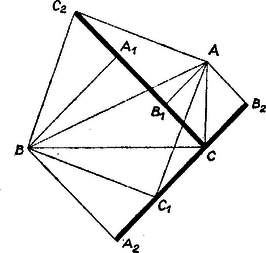

2. ábra

3. ábra

Derékszögű háromszögből kiindulva itt is elfajulások állnak be (3. ábra).
Berács József (Győr, Czuczor G. g. II. o. t.) dolgozatából kiegészítésekkel

Megjegyzés. Szabályos háromszögben az I. eset pontrendszere csak

6

pontból áll, és

3

paralelogrammát tartalmaz. Az említett elfajulásokkal szemben egyes speciális esetekben viszont újabb paralelogrammák léphetnek fel, pl. az I. esetben a

30^{\circ}

60^{\circ}

90^{\circ}

, a

30^{\circ}

30^{\circ}

120^{\circ}

szögű háromszögben.