Kezdőlap


Feladat:	1030. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Murvai Éva , Nagy Kálmán , Tátray Péter
Füzet:	1966/november, 146 - 147. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Egyenlő szárú háromszögek geometriája, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1966/január: 1030. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mérjük rá a $B D$ oldal meghosszabbítására a $D F = B C = B A$ szakaszt. Ekkor $B F = B D + D F = A E + B A = B E$ , és mivel $F B E ∢ = 60^{\circ}$ , $B F E$ egyenlő oldalú háromszög, $E F = E B$ , és $E F B ∢ = 60^{\circ}$ . Így pedig $E D F Δ ≃ E C B Δ$ , tehát $E D = E C$ .

Tátray Péter (Budapest, Berzsenyi D. g. II. o. t.)

II. megoldás. Mérjük föl a

B A

félegyenesre a

B G = B D

szakaszt. A bizonyítandó egyenlőség következik, ha belátjuk, hogy

E C A

és

D E G

egybevágó háromszögek. Ez valóban fennáll, mert

E A = B D = D G

hiszen

B D G

egyenlő oldalú háromszög, és ugyanezért

E A C ∢ = 120^{\circ} = D G E ∢

, valamint

A C = A B = E B - E A = E B - B G = G E

. Ezzel az állítást bebizonyítottuk.

Nagy Kálmán (Celldömölk, Berzsenyi D. g. I. o. t.)

III. megoldás. Legyen a

C D

szakasz felezőpontja

H

, és mérjük rá a

B A

félegyenesre a

B K = B H

szakaszt. Ekkor

K E = B E - B K = B A + A E - B H = B C + B D - (B C + C H) = B D - D H = B H = B K

, másrészt

K H = K B

, mert

B H K

egyenlő oldalú háromszög. Eszerint

H

rajta van a

B E

szakasz mint átmérő fölötti Thalész-körön, a

C D E

háromszög

E H

súlyvonala merőleges a

C D

oldalra, így e háromszög egyenlő szárú, qu. e. d.

Murvai Éva (Makó, József A. g. II. o. t.)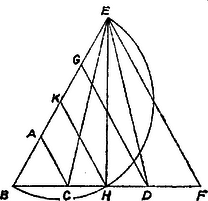

Megjegyzés. A legutóbbi megállapítást,

C H

és

E H

merőleges voltát abból is kimondhatjuk, hogy

E B H ∢ = 60^{\circ}

és

B E = 2 B K = 2 B H

miatt a

B E H

háromszög egy egyenlő oldalú háromszög fele.