Kezdőlap


Feladat:	1029. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Berács J. , Bolgár G. , Csirmaz L. , Dobos K. , Futó Ilona , Gegesy F. , Geier J. , Hegedűs András , Hernádi Ágnes , Horváth Gergely , Jobbágy T. , Karger Kocsis J. , Moson P. , Munk S. , Pap Márta , Perémy G. , Pintz J. , Rajczy P. , Sax Gy. , Szilléry A. , Takács L. , Tóth Péter , Vályi I.
Füzet:	1966/november, 144 - 146. oldal		PDF \| MathML
Témakör(ök):	Irracionális számok és tulajdonságaik, Algebrai átalakítások, Interpolációs polinomok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1966/január: 1029. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Egyelőre az $a > 0$ esetre szorítkozunk. A feltevés szerint $a^{2} < a^{2} + b < a^{2} + 2 a + 1 = {(a + 1)}^{2}$ , ezért a $C = a^{2} + b$ kifejezés négyzetgyökének $c$ abszolút értéke $a$ és $a + 1$ közé esik, tehát a gyök első közelítő értékének vehető $c_{1} = a$ , és ez éppen az (1) kifejezés első tagja. Ez megfelel annak, hogy a négyzetgyökvonás idézett eljárásában első lépésül két szomszédos, a $C$ -t közrefogó teljes négyzetet keresünk, és a kisebbikük alapját vesszük első számjegynek.
Az idézett eljárásban a gyök közelítő értéke számára a további, egyre kisebb helyi értékű számjegyeket már mindig osztással állapítjuk meg, a maradékot osztjuk a gyök már meglevő közelítő értékének $2$ -szeresével. Az első maradék $C$ -ből az első közelítő érték kivonásával áll elő, esetünkben $m_{1} = b$ , a mondott hányados $d_{1} = m_{1} / 2 c_{1} = b / 2 a$ ‐ és ez éppen az (1) második tagja ‐, és a második közelítő érték

\begin{matrix} c_{2} = a + d_{1} = a + \frac{b}{2 a} = \frac{2 a^{2} + b}{2 a} . \end{matrix}

A második maradékot úgy kapjuk, hogy az első maradékból kivonjuk az új taggal (jeggyel) megnövelt első osztónak és az új tagnak a szorzatát:

\begin{matrix} m_{2} = m_{1} - (2 c_{1} + d_{1}) \cdot d_{1} = - d_{1}^{2} = - \frac{b^{2}}{4 a^{2}}, \end{matrix}

(ugyanerre vezet

C - c_{2}^{2}

is). Az eljárást folytatva a második maradéknak és a második közelítő érték

2

-szeresének hányadosa adja a gyök harmadik tagját:

\begin{matrix} d_{2} = \frac{m_{2}}{2 c_{2}} = - \frac{b^{2}}{4 a^{2}} : \frac{2 a^{2} + b}{a} = - \frac{b^{2}}{4 a (2 a^{2} + b)}, \end{matrix}

a gyök harmadik közelítő értéke

c_{3} = a + d_{1} + d_{2}

, ez pedig azonos (1)-gyel. Ezt kellett bizonyítanunk.
Most már hasonlóan a harmadik maradék, a harmadik osztó és a harmadik hányados rendre:

\begin{matrix} m_{3} = m_{2} - (2 c_{2} + d_{2}) \cdot d_{2} = - d_{2}^{2} = - \frac{b^{4}}{16 a^{2} {(2 a^{2} + b)}^{2}}, \\ 2 c_{3} = 2 a + \frac{b}{a} - \frac{b^{2}}{2 a (2 a^{2} + b)} = \frac{8 a^{2} (a^{2} + b) + b^{2}}{2 a (2 a^{2} + b)}, \\ d_{3} = - \frac{b^{4}}{8 a (2 a^{2} + b) [8 a^{2} (a^{2} + b) + b^{2}]}, \end{matrix}

és a kívánt negyedik tag

d_{3}

.
A feltevés megengedi a

- 1 / 2 < a < 0

értékeket is, ilyen

a

esetén a

(- 1)

-szeresét kapjuk annak a közelítő értéknek, ami

| a |

alapján adódott volna.
(Másrészt némi eltérés is mutatkozik (1) tagjainak és az idézett eljárásban a gyök közelítő értéke számjegyeinek képzése között, az, hogy

c_{2}

c_{3}

c

-nek felső közelítő értéke (hiszen

m_{2}

m_{3}

negatív, tehát

c_{2}^{2}

c_{3}^{2} > C

), míg határozott számok esetén, a tízes számrendszerben számolva mindig alsó közelítő értéket képezünk a négyzetgyökre. Erre az alábbi megjegyzésben még visszatérünk.)
A

- 2 a + 1 < b < 0

esetben

\begin{matrix} a^{2} > a^{2} + b > a^{2} - 2 a + 1 = {(a - 1)}^{2}, \end{matrix}

eszerint

a > c > a - 1

, és már

c_{1} = a

is fölső közelítő érték, és

m_{1} = b

is negatív; (1) természetesen így is érvényes. Itt a feltevés miatt

a > 1 / 2

, ezért (1) mindig a négyzetgyök pozitív értékét adja.
II. Az

α

) adatpár esetében

C = 51

, és (1) értéke, valamint a keresett eltérés

\begin{matrix} c_{3} = 7 + \frac{2}{14} - \frac{4}{2800} = 7 + \frac{1}{7} - \frac{1}{700} = 7 \frac{99}{700} = \frac{4999}{700}, \\ C - c_{3}^{2} = 51 - \frac{4999^{2}}{700^{2}} = - \frac{1}{700^{2}} = - d_{2}^{2}, \end{matrix}

éppen az (1) képezése után adódott maradék, aminek így is kellett lennie. ‐ Hasonlóan a

β

) adatpár esetében

C^{*} = 61

\begin{matrix} c_{3}^{*} = 8 - \frac{3}{16} - \frac{9}{4000} = 7 \frac{3241}{4000} = \frac{31 241}{4000}, \\ C^{*} - c_{3}^{* 2} = - \frac{81}{4000^{2}} = - {(\frac{9}{4000})}^{2} = - d_{2}^{*} . \end{matrix}

III. Tizedes alakú közelítő értékekkel

\begin{matrix} \sqrt[]{51} = 7, 141 428 4 ..., c_{3} = 7, 141 428 5 ...; \\ \sqrt[]{61} = 7, 810 249 6 ..., c_{3}^{*} = 7, 810 25, \end{matrix}

ezekben a példákban (1) három tagja a négyzetgyökből

7

, ill.

6

számjegyet adott meg helyesen.

Hegedüs András (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

Megjegyzések. 1. Nem lényeges, hogy egy számot alsó vagy fölső közelítő értékével közelítünk meg, ha ennek a pontos értéktől való eltérése kisebb a megengedett hibahatárnál. A számjegyenként való számolásnál azért kényelmesebb mindig az alsó közelítő érték, a még pozitív maradékot hagyó legnagyobb számjegy keresése, mert ezt a később megállapítandó számjegyek már nem változtatják meg, szemben a fenti példák

c_{1} = 7

c_{2} = 7, 1428 ...

c_{3} = 7, 1414 ...

, ill.

c_{1}^{*} = 8

c_{2}^{*} = 7, 8125

c_{3}^{*} = 7, 8102

csökkenéseivel. ‐ Egyébként általános alakban nem is lehet közelítő értéket adni, pl. a

b / 2 a

hányadoshoz.
Ami a számjegyenkénti eljárás lassabb haladását illeti, ez csak kényelmi kérdés. Lehetne egy csapásra két új számjegyet is próbálni a gyökből, de így nehézkesebb lenne képezni és leíratlanul mindjárt ki is vonni az új résszel kiegészített kétszeres osztó és az új rész szorzatát.
2. Az (1) első két tagját így is értelmezhetjük. Ha egy (pozitív) számot osztunk a négyzetgyökével, a hányados is egyenlő a négyzetgyökkel. Osztóként a négyzetgyöknek egy alsó közelítő értékét véve, a hányados nagyobb az előbbinél, tehát fölső közelítő értéke a négyzetgyöknek; és fordítva: fölső közelítő értékkel osztva alsó közelítő értéket kapunk hányadosul. Mindkét esetben várható, hogy az osztó és a hányados számtani középértéke mindegyiküknél közelebb áll a keresett négyzetgyökhöz. Esetünkben

c_{1} = a

és

(a^{2} + b) / a = a + b / a

középértéke

a + b / 2 a

. ‐ Így mindig fölső közelítő értéket kapunk, mert az osztó és a hányados mértani közepe éppen a keresett gyök, és a számtani közép nagyobb a mértaninál.
Azt is kapjuk, hogy a vett számtani közép hibája ‐ a valódi értéktől való eltérése ‐ kisebb, mint a közép eltérése az alsó közelítő értéktől, vagyis legfeljebb fele akkora, mint a felső és az alsó közelítő érték különbsége, esetünkben

b / 4 a

abszolút értéke.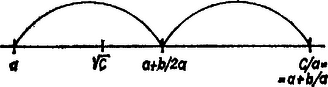

Egyszerű számítás mutatja, hogy hasonlóan

c_{3}

ismét számtani közepe

c_{2}

-nek és

(a^{2} + b) / c_{2}

,-nek, és hogy hibája kisebb, mint (1) harmadik tagja felének abszolút értéke.