Kezdőlap


Feladat:	1025. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Cserha Gabriella
Füzet:	1966/október, 73 - 75. oldal		PDF \| MathML
Témakör(ök):	Pont körüli forgatás, Derékszögű háromszögek geometriája, Beírt kör, Terület, felszín, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1965/december: 1025. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Legyen az $A_{1} B_{1} C = D_{1}$ derékszögű háromszögben $B_{1} C = a \leq C A_{1} = b < A_{1} B_{1} = c$ , és forgassuk $D_{1}$ -et $C$ körül az $A_{2} B_{2} C = D_{2}$ helyzetbe úgy, hogy $A_{2}$ a $C B_{1}$ félegyenesen legyen; ekkor $B_{2}$ az $A_{1} C$ félegyenesen van, $B_{1}$ pedig az $A_{1} A_{2} B_{2}$ háromszög belsejében, vagy azonos $A_{2}$ -vel. (A forgatás iránya nem lényeges, mert az 1, 2 indexeket felcserélve $D_{1}$ ellentétes irányú fordulással jut $D_{2}$ -be, és a vizsgálandó alakzat csúcspontjai mégis ugyanazok a pontok.)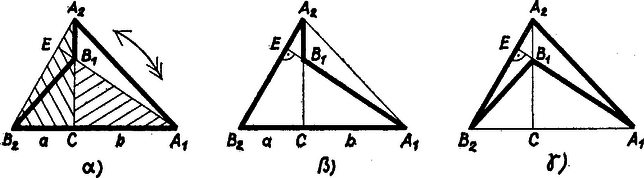

1. ábra

A_{1} A_{2} B_{1} B_{2} = N_{1}

négyszög (1. ábra

α

része) két átlója a

D_{1}

és

D_{2}

átfogója, így egyenlők és a forgatás miatt merőlegesek. Messe az

A_{1} B_{1}

egyenes

A_{2} B_{2}

-t

E

-ben, ekkor, idomok területét ugyanúgy jelölve, mint magukat az idomokat:

\begin{matrix} N_{1} = A_{1} B_{1} A_{2} + A_{1} B_{1} B_{2} = \frac{A_{1} B_{1} \cdot A_{2} E}{2} + \frac{A_{1} B_{1} \cdot E B_{2}}{2} = \\ = \frac{A_{1} B_{1}}{2} (A_{2} E + E B_{2}) = \frac{A_{1} B_{1} \cdot A_{2} B_{2}}{2} = \frac{c^{2}}{2}, \end{matrix}

másrészt a

B_{1} C

szakasz mentén kettévágva

\begin{matrix} N_{1} = A_{1} A_{2} C + B_{1} B_{2} C = \frac{b^{2}}{2} + \frac{a^{2}}{2}, \end{matrix}

és e két előállítás egyenlősége Pitagorasz tételét adja. ‐ A

b = a

esetében

B_{1}

azonos

A_{2}

-vel és

E

-vel is, így

N_{1}

elfajul az

A_{1} B_{1} B_{2}

egyenlő szárú derékszögű háromszöggé, és a bizonyítás még egyszerűbbé válik.
Felhasználtuk a következő tételeket: forgatás változatlanul hagyja az idom oldalait és szögeit, részekre bontott idom területe egyenlő összes részei területének összegével, továbbá a háromszög területképletét. Egyik tétel bizonyításában sem használtuk fel a bizonyítandó tételt, így bizonyításunk helyes.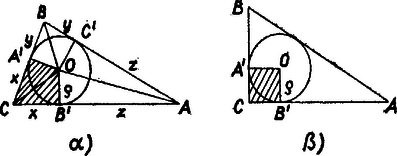

II. A beírt kör sugarának ajánlott kifejezése így alakítható:

\begin{matrix} ϱ = \frac{s}{2} - c = \frac{1}{2} (a + b - c) . \end{matrix}

Ezt az ajánlott területképletbe beírva, másrészt a területet a befogókkal is kifejezve

\begin{matrix} t = s ϱ = \frac{1}{2} (a + b + c) \cdot \frac{1}{2} (a + b - c) = \frac{1}{4} [{(a + b)}^{2} - c^{2}] = \frac{1}{2} a b, \end{matrix}

amiből átrendezéssel

a^{2} + b^{2} = c^{2}

2. ábra

t = ϱ s

képlet a háromszög három,

ϱ

magasságú háromszögre bontásából adódik (2. ábra

α

része) ‐ alapjaik az egyes oldalak ‐ ezekre alkalmaztuk a területképletet. A sugár képlete abból adódik, hogy a kör

O

középpontja, a háromszög egy csúcsa, és a belőle húzott érintők érintési pontjai, pl.

C

A'

és

B'

, mindig egy deltoid csúcsai, az érintőszakaszok egyenlők, együttes hosszuk a kerületből az

A B

oldal kétszeresének elhagyásával adódik, továbbá hogy

A C B ∢ = 90^{\circ}

esetén e deltoid négyzetté specializálódik (2. ábra

β

része), oldalai egyenlők. Ezekben sem használtuk fel Pitagorasz tételét.

Cserha Gabriella (Makó, József A. g. I. o. t.)

Megjegyzések. Az I. részben az

A_{1}

B_{1}

A_{2}

B_{2}

csúcsokat két további sorrend szerint bejárva ugyancsak konkáv négyszöget kapunk. Ezekből is kapunk egy-egy, a fentitől különböző bizonyítást.
Az

A_{1} B_{1} A_{2} B_{2} = N_{2}

négyszög területét (1. ábra

β

része) egyrészt

D_{1}

és

D_{2}

összegeként, másrészt az

A_{1} A_{2} B_{2}

és

A_{1} A_{2} B_{1}

háromszögek különbségeként állítjuk elő.

A_{2} B_{1} E

és

D_{1}

hasonlók, ezért

\begin{matrix} B_{1} E = e = \frac{B_{1} A_{2}}{B_{1} A_{1}} \cdot B_{1} C = \frac{a (b - a)}{c}, A_{1} E = c + e = \frac{c^{2} + a b - a^{2}}{c}, \\ N_{2} = A_{1} A_{2} B_{2} - A_{1} A_{2} B_{1} = \frac{c \cdot A_{1} E}{2} - \frac{b (b - a)}{2} = 2 D_{1} = a b, \\ \frac{1}{2} (c^{2} + a b - a^{2} - b^{2} + a b) = a b, \end{matrix}

és ez rendezéssel a tételt adja. ‐ A fenti tételeken túl felhasználtuk, hogy két idom különbségeként előálló idom területe egyenlő azon idomok területének különbségével, és hogy hasonló idomok megfelelő oldalainak aránya egyenlő.
Végül az

A_{1} A_{2} B_{2} B_{1} = N_{3}

négyszögre (1. ábra

γ

része) hasonlóan

\begin{matrix} N_{3} = A_{1} A_{2} B_{2} - A_{1} B_{1} B_{2} = A_{1} A_{2} B_{1} + B_{2} A_{2} B_{1} = \frac{B_{1} A_{2} \cdot A_{1} B_{2}}{2}, \\ c (c + e) - a (a + b) = c^{2} - 2 a^{2} = b^{2} - a^{2}, \end{matrix}

ezt kellett bizonyítanunk.

B_{1} = A_{2}

esetén

N_{3}

területe 0.