Kezdőlap


Feladat:	1014. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berács J. , Bulkai Tamás , Futó Ilona , Gyarmati Erzsébet , Hernádi Ágnes , Horváth S. , Kuluncsich T. , Lakner Mária , Munk S. , Papp Emma , Püski Anna , Szenes Katalin , Szűcs A. , Takács L.
Füzet:	1966/szeptember, 20 - 22. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Trapézok, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1965/november: 1014. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az adott szakaszokból kétféleképpen állíthatók össze egy trapéz oldalai. Az 5 cm-es szakasz mindkétszer alap lesz, a másik alap pedig vagy 20 vagy 15 cm. Ugyanis a trapéz felbontható egy paralelogrammára és egy háromszögre, az utóbbinak két oldala egyenlő a trapéz száraival, a harmadik pedig a trapéz alapjainak különbségével, emiatt a két alap különbségének nagyobbnak kell lennie a két szár különbségénél. Ez azonban nem teljesül, ha az 5 cm-es szakaszt szárnak próbáljuk.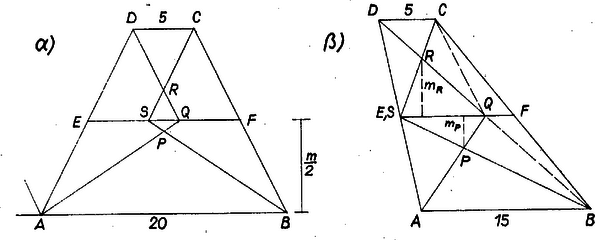

Legyen mindkét esetben az

A B C D = T

trapézban

A B ∥ C D

, a kérdéses négyszög

P S R Q = N

úgy, hogy

P

-ben a

D A B

és

A B C

szögek felezői metszik egymást s i. t., és az

A D

B C

szár felezőpontja

E

, ill.

F

. A

Q

S

pontok az

E F

középvonalon vannak, mert a szögfelező pontjainak tulajdonságánál fogva, pl.

Q

A B

-től is,

C D

-től is ugyanakkora távolságra van, ti. annyira, mint

A D

-től, tehát a távolság fele a trapéz

m

magasságának. Másrészt

P Q R

és

P S R

derékszögek, mert pl. az

A D C

szög felezője párhuzamos az

A

-nál levő külső szög felezőjével, és így merőleges

A Q

-ra. Így a kérdéses négyszög húrnégyszög. ‐ Továbbá

Q

rajta van az

A D

átmérő fölötti Thalész-körön,

Q E = A D / 2

, és ugyanígy

S F = B C / 2

. Ezek alapján

Q S

kiszámítható, egyenlő

E Q + S F = (A D + B C) / 2

és

E F = (A B + C D) / 2

különbségének abszolút értékével.
Amennyiben

Q

és

S

nem esnek egybe,

P

és

R

Q S

, azaz

E F

egyenes két különböző partján adódik, ezért

Q S

N

-et a

Q S P

és

Q S R

háromszögekre osztja, ezeknek

Q S

-re merőleges

m_{P}

m_{R}

magassága kifejezhető annak alapján, hogy pl.

A B P

és

Q S P

hasonló háromszögek:

\begin{matrix} m_{P} = \frac{m}{2} \cdot \frac{Q S}{A B \pm Q S}, hasonlóan m_{R} = \frac{m}{2} \cdot \frac{Q S}{Q S \pm C D} \end{matrix}

(a kettős előjelek közül az alsók akkor érvényesek, ha a pontok a középvonalon

E

Q

S

F

sorrendben adódnak). Így pedig

N

területe

\begin{matrix} \frac{1}{2} \cdot Q S (m_{P} + m_{R}) = \frac{m \cdot Q S^{2}}{4} (\frac{1}{A B \pm Q S} + \frac{1}{C D \pm Q S}) . \end{matrix}

Másrészt

T

területe

m \cdot E F = m (A B + C D) / 2

, így a keresett arányszám

\begin{matrix} k = \frac{Q S^{2}}{2 (A B + C D)} (\frac{1}{A B \pm Q S} + \frac{1}{C D \pm Q S}) . \end{matrix}

Mármost I.

A B = 20

C D = 5

A D = B C = 15

esetén (az ábra

α

része)

E F = 12, 5

E Q = F S = 7, 5

Q S = E Q + S F - E F = 2, 5

, és így

\begin{matrix} k_{I} = \frac{2, 5^{2}}{50} (\frac{1}{22, 5} + \frac{1}{7, 5}) = \frac{1}{45} . \end{matrix}

Ebben az esetben

T

, és vele

N

is, szimmetrikus az

A B

felező merőlegesére,

N

húrdeltoid.
II.

A B = A D = 15

C D = 5

B C = 20

esetén pedig (

β

ábrarész)

E F = 10 = F S

S

azonos

E

-vel, így

Q S = E Q = 7, 5

és

k_{II} = 7 / 40

Bulkai Tamás (Győr, Bencés g. II. o. t.) dolgozatából összevonással

Megjegyzés. Az I. esetben a szimmetriára és az adódó

60^{\circ}

-os szögekre támaszkodva egyszerűbb számítás lehetséges, a fenti megoldás viszont mindkét esetet egyszerre intézi el.