| Feladat: | 1009. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: átlagos |
| Megoldó(k): | Berács J. , Bozóky-Szeszich Ádám , Csirmaz L. , Horváth S. , Kóczy L. , Koren András , Kovács Tamás , Mérő L. , Pintz J. , Sax Gy. , Siklósi I. , Szeredi P. , Takács L. | ||
| Füzet: | 1966/október, 66 - 68. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkidomok átdarabolása, Egyenlő szárú háromszögek geometriája, Terület, felszín, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1965/október: 1009. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen az adott háromszög , az adott belső pont az oldalon , a oldalon . Előírhatjuk, hogy az első vágás -ből induljon ki; ennek egyik oldalán 1, a másikon 2 résznek kell lennie, tehát a háromszög területét 1:2 arányban kell kettévágnia. Forgassunk egy félegyenest körül a helyzetből kiindulva, -n át a helyzetig és tekintsük a háromszögből a félegyenes két oldalára eső részek területének arányát. Az -t tartalmazó rész területe egyre nő, a másiké fogy, így az arány tetszés szerinti kicsiny (pozitív) értéktől tetszés szerinti nagy értékig minden értéket felvesz, és csak egyszer, tehát az 1/2 és a 2/1 értéket is, így első vágásként a félegyenes két helyzete felel meg. E két helyzet az alábbiak szerint szerkeszthető. 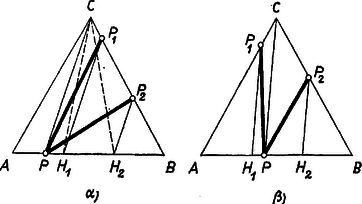 Legyenek az oldal harmadoló pontjai , úgy, hogy . Húzzunk párhuzamost -en és -n át a egyenessel, és messék ezek az törött vonaldarabot -ben, ill. -ben. Ekkor és a megfelelő vágások. Legyen ugyanis először az oldal egyik szélső harmadán, mondjuk -en, akkor , mindegyike és között adódik (esetleg , ha ti. ), mert és kiindulópontja és között van (1. ábra része). A területe , a -é pedig , mert az előbbi egyenlő a , az utóbbi a területével, ezeknek -vel közös az -re merőleges magasságuk, alapjuk pedig , ill. , és így területük , ill. . Valóban, a és háromszögek () része közös, és a egyenes másik partján levő részeik területe is egyenlő, mert a alapjuk közös, és erre merőleges magasságuk egyenlő. Így a területe is és az négyszög területe is . A -re adott bizonyításunk akkor is érvényes, ha a szakaszon van, mert ilyenkor is -n adódik (1. ábrarész). Ilyen esetben az -n van, és a területe a -ével egyenlő, ez is . A talált két vágási lehetőség közül számunkra az lesz megfelelő, amelyik a második kiinduló pontot a kettévágott háromszög nagyobb részébe juttatja. A két vágás közül legalább az egyik ilyen; ha pedig így mindkettő megfelel, akkor és bármelyikét vehetjük első vágásszakasznak. A kiszemelt vágás a háromszöget egy háromszögre és egy (konvex) négyszögre vágja szét (vagy kivételesen 2 háromszögre, ha ti. éppen -ben vagy -ben van). Így már csak azt kell megmutatnunk, hogy háromszöget is, négyszöget is lehet két egyenlő részre vágni a kerületének adott pontjából kiinduló egyenes vágással, hiszen kerületi pontja a levágott 2/3 résznek. 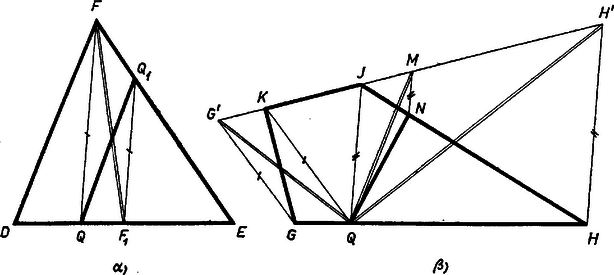 Legyen a oldalának pontja. Húzzunk párhuzamost a oldal felezőpontján át -fel, ez metszi ki a háromszög kerületéből a vágás végpontját (2. ábra része), mert , . Legyen a négyszög oldalán és messük -t a -n átmenő, -val párhuzamos egyenessel -ben, valamint a -n átmenő, -vel párhuzamos egyenessel -ben (2. ábrarész). A fentiekhez hasonlóan látható, hogy a négyszög területe egyenlő a -ével, és hogy az utóbbit megfelezi a szakasz felezőpontját -val összekötő egyenes vágás, ami egyszersmind a négyszöget is felezi, amennyiben a szakaszon adódik. Az ellenkező esetben válasszuk a betűzést úgy, hogy a szakaszra essék. Ekkor a négyszög területe kisebb a négyszög területének felénél, mert az utóbbi a területével egyenlő, az előbbi pedig a -ével. Különbségük a . Ezzel egyenlő területet úgy vághatunk le a négyszög további részéből, a -ből, hogy az -en átmenő, -vel párhuzamos egyenesnek -vel való metszéspontjába irányítjuk a -ból kiinduló vágást; így ugyanis a területe egyenlő a különbözettel. Minden lehetséges esetre eljárást adtunk a második vágás végpontjának kijelölésére, a feladatot megoldottuk. Amennyiben az első vágást -ból indítjuk el, lehetséges, hogy más két vágást kapunk. Ezt a kérdést azonban nem vizsgáljuk, mert a feladat nem írja elő a , pontpárból lehetséges összes vágáspárok előállítását. Sehol nem használtuk ki az egyenlő oldalú voltát, sem -nek és -nak , , -től, valamint egymástól különböző voltát, így eljárásunk bármely háromszög kerületén bárhogyan választott két kiindulási vágáspont esetén érvényes. Bozóky-Szeszich Ádám (Budapest, Berzsenyi D. g. II. o. t.) |