| Feladat: | 1007. matematika gyakorlat | Korcsoport: 14-15 | Nehézségi fok: könnyű |
| Megoldó(k): | Aczél Klára , Balázs Dénes | ||
| Füzet: | 1966/szeptember, 18. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Terület, felszín, Paralelogrammák, Alakzatok köré írt kör, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1965/október: 1007. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Ha valamelyik háromszögről megmutatjuk, hogy területe a másik három háromszög területének összegével egyenlő, ezzel azt is megmutattuk, hogy ez a legnagyobb területű. 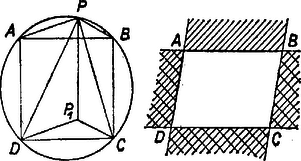 Legyen a körön választott pont a négyzet oldala fölötti negyedkörön; a négyzet további csúcsai legyenek és . Toljuk el az háromszöget úgy, hogy az oldal -re kerüljön, új helyzete legyen. Ekkor ‐ a háromszögek területeit ugyanúgy jelölve, mint a háromszöget ‐ nyilván , továbbá az egy-egy átlójukkal kettévágott és paralelogrammából és . Így Ezzel a feladat állítását bebizonyítottuk, sőt annál jóval többet is, hiszen a bizonyításban csak annyit használtunk ki, hogy paralelogramma (még azt sem, hogy szögei derékszögek), továbbá hogy az oldal és a , oldalak meghosszabbítása határolta tartományban (sávban) van. (Az ábrán egyszer vonalkázva.) A betűk megfelelő cseréjével alkalmazható a bizonyítás az ábra kétszer vonalkázott sávjaira is. Ha a pont határvonalon van, egy vagy két háromszög egyenesszakasszá fajul, területéül 0 veendő. Aczél Klára (Budapest, Fazekas M. gyak. g. I. o. t.) |