Feladat: 999. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Bozóky Szeszich Ádám ,  Csáki István ,  Feledi Ildikó ,  Fűrész József ,  Jancsó Annamária ,  Muzsnai László ,  Pócsik István 
Füzet: 1966/március, 120 - 121. oldal  PDF  |  MathML 
Témakör(ök): Síkidomok átdarabolása, Terület, felszín, Sokszögek szimmetriái, Gyakorlat
Hivatkozás(ok):Feladatok: 1965/szeptember: 999. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Húzzuk meg az adott S12 szabályos tizenkétszög oldalfelező merőlegeseit. Ezek az O középpontban metszik egymást, az oldal felezőpontjától O-ig terjedő szakaszuk egyenlő, és bármely két szomszédos oldalhoz tartozó ilyen szakasz között ugyanakkora szög van, a teljes szög 12-ed része.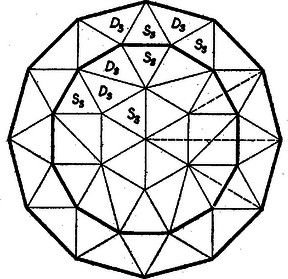

 
 

Bármelyik oldal fölé rajzolt S3 szabályos háromszög új csúcsa az oldalfelező merőlegesen, az előbbi szakasz meghosszabbításán adódik, az oldaltól mindig ugyanakkora távolságban. Ezért bármelyik új csúcsot O körül a teljes szög 12-ed részével elforgatva a szomszédos oldal fölé rajzolt S3 új csúcsába jut át. Így a 12 új csúccsal meghatározott T12 tizenkétszög valóban szabályos.
 

II. S12 mindegyik szöge 150∘, ez és a bezáró oldalakra rajzolt két S3 a csúcsnál 150∘+2⋅60∘=270∘ szögtartományt fed le, így az új csúcsok szomszédos párjainak összekötésével keletkező D3 háromszögek S12-vel közös csúcsánál 90∘-os szög van. Ezért az S12 és T12 közti gyűrű alakú idom 12 db S3-ból és 12 db egybevágó egyenlő szárú derékszögű D3-ból áll, ugyanis mindegyik D3 befogója egyenlő S12 oldalával.
 
Rajzoljunk S12 minden második oldala, mint alap fölé, befelé S3 szabályos háromszögeket. Ezek új oldalai 150∘-60∘=90∘-os szöget zárnak be S12-nek avval a csatlakozó oldalával, amelyre befelé nem rajzoltunk S3-at. Ezért a 6 új csúcsot egymás után összekötve, a kihagyott oldalak fölött 6 egybevágó négyzetet kapunk, középen pedig egy S6 szabályos hatszög adódik, mert S12-nek a teljes szög 2/12-ed részével való forgatása az újabb S3-akat egymásba viszi át.
 

Húzzuk meg S6 3 leghosszabb átlóját és a 6 négyzet 1‐1 átlóját. Így S6-ot 6 db S3-ra, és mindegyik négyzetet 2 db D3-ra osztottuk. Eszerint S12 ugyanúgy 12 db S3-ból és 12 db D3 ból áll, mint a gyűrű‐idom. Ezzel az állítást bebizonyítottuk.
 
Feledi Ildikó (Nagykanizsa, Landler J. g. II. o. t.)
Muzsnai László (Debrecen, Református Koll. g. I. o. t..)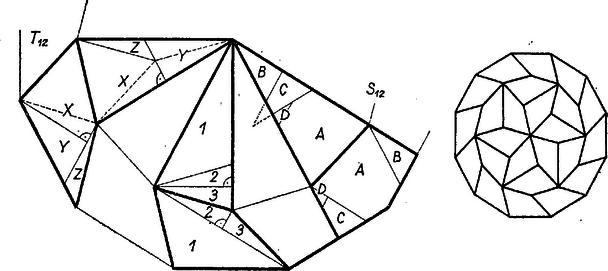

 
Megjegyzések 1. A területek egyenlőségét számítással is bizonyíthatjuk. Azt mutatjuk meg, hogy T12 területe 2-szer akkora, mint S12-é. T12 hasonló S12-höz, ezért területeik aránya egyenlő oldalaik négyzetének arányával. Oldaluk D3-nak átfogója. ill. befogója, D3 átfogójának négyzete viszont Pitagorasz tétele értelmében 2-szerese a befogó ‐ vagyis S12 oldala ‐ négyzetének.
 
Bozóky‐Szeszich Ádám (Budapest, Berzsenyi D. g. II. o. t.)

 
 

2. A 2.a ábrán 3 átdarabolásos bizonyítást vázolunk S12 és a gyűrű‐idom 1/12 része területének egyenlőségéhez. Az egyformán jelölt darabok egybevágóságának bizonyítását az olvasóra hagyjuk. Az 1, 2, 3 jelű felbontást Csáki István (Szolnok, Verseghy F. g. II. o. t.) és Jancsó Annamária (Budapest, Fazekas M. gyak. g. II. o. t.), az X, Y, Z jelűt Fürész József (Tatabánya, Árpád g. III. o. t.), az A, B, C, D jelűt Pócsik István (Eger, Gárdonyi G. g. III. o. t.) dolgozatából közöljük, némi egyszerűsítéssel.
 
3. Tetszetős átdarabolást mutat a 2.b ábra, minden négyszöge egy D3 és egy S3 egybekapcsolásával áll elő. Az S12 2‐2 oldalára támaszkodó négyszögek tükrösen egybevágók a belső négyszögekkel.