| Feladat: | 992. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Füzet: | 1966/április, 166 - 168. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Alakzatba írt kör, Másodfokú (és arra visszavezethető) egyenlőtlenségek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1965/május: 992. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. Legyenek az eredeti -lemez oldalai és , ahol . Ekkor a belőle egy darabban kivágható legnagyobb körlemez átmérője nyilvánvalóan . Ilyenből 2 db is kivágható, ha (1. a ábra), különben azonban nem. 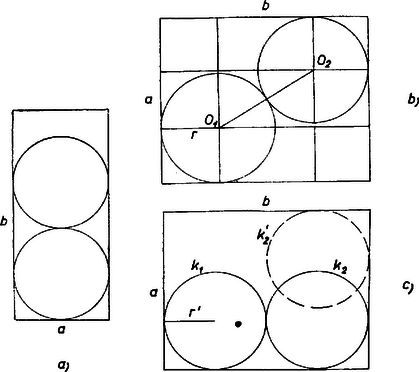 Az 1. b ábrán a két középpont távolsága annak a téglalapnak az átlója, melynek oldalai oldalaitól távolságban haladnak, -n belül. Ennek oldalai és , ennélfogva és így a legnagyobb körlemez-pár átmérője 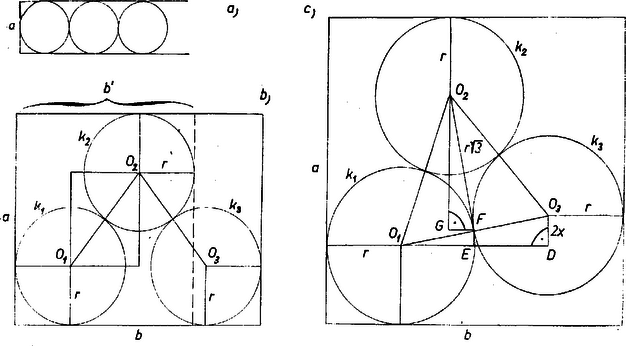 II. Hasonlóan adódik, hogy esetén lehet -ből kivágni db átmérőjű körlemezt, valamint hogy esetén a 2. b ábra szerinti elrendezésben nagyobb átmérőjű körlemezek várhatók, mint . Mondhatjuk, hogy a 2. b ábrán két egyenlő sugarú kör van kivágva a alapú, magasságú téglalapból, így az -et megadó egyenlet (1)-ből adódik, helyére -t írva: A négyzetgyökjel előtt jelet véve a másik gyök , pozitív, ezért a felírt is pozitív, hiszen szorzatuk, az egyenlet -et nem tartalmazó tagja, pozitív. Egyébként a gyökök nyilvánvalóan valósak. Állandó és egyre rövidülő esetén az alapon levő két kör mindaddig nem nyúlik egymásba, amíg . Ennek feltétele (2) alapján ill. a korábbi korlátozást is figyelembe véve A hátra levő esetben mindhárom kör páronként érinti egymást, viszont a kör már csak az hosszúságú oldalt érinti. A 2. c ábra jelöléseivel A négyzetgyököt (4)-ből kifejezve és (3)-ba helyettesítve A diszkrimináns, végül a körök sugara Speciálisan, esetén, figyelembe véve, hogy |