Kezdőlap


Feladat:	990. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kovács M. , Takács László , Tolnay-Knefély T.
Füzet:	1966/szeptember, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Körülírt kör, Gyakorlat, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1965/május: 990. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A $P$ -ben meghúzott érintők közti négy szög közül bármelyikük meghatározza a többiek nagyságát. Azt a szöget fogjuk tekinteni, melynek szárai ‐ ún. félérintők ‐ az $A B$ egyenesnek $C$ -t nem tartalmazó partján haladnak.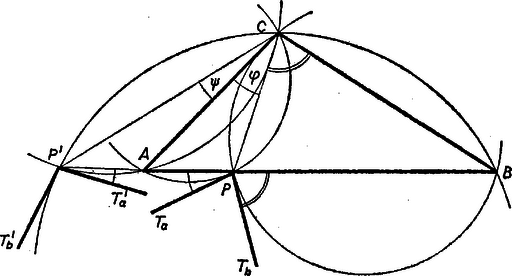

Legyen

P

A B

oldalszakasz belső pontja,

P C A ∢ = φ

A C B ∢ = γ

, és az előírt félérintők egy-egy

P

-től különböző pontja rendre

T_{a}

T_{b}

. Ekkor

A P T_{a} ∢ = φ

, mert a

P A C

háromszög köré írt körben a

C

-t nem tartalmazó

A P

íven nyugvó kerületi szög. Hasonlóan

T_{b} P B ∢ = P C B ∢ = γ - φ

; ennek

P B

szára ellentétes irányú

P A

-val, így

\begin{matrix} T_{a} P T_{b} ∢ = 180^{\circ} - A P T_{a} ∢ - T_{b} P B ∢ = 180^{\circ} - γ . \end{matrix}

Ha a mozgó pont az

A B

oldal

A

-n túli meghosszabbításán levő

P'

pontban van, legyen

P' C A ∢ = ψ

. Így az előzőkhöz hasonlóan

T_{a}' P' A ∢ = ψ

T_{b}' P' B ∢ = P' C B ∢ = ψ + γ

, és mivel

P' A

és

P' B

száruk egybeesik,

\begin{matrix} T_{b}' P' T_{a}' ∢ = T_{b}' P' B ∢ - T'_{a} P' A ∢ = γ . \end{matrix}

Megállapításunk akkor is érvényes, amikor

P

éppen áthalad

A

-n, ha ekkor az első kör helyett a

C

-n átmenő és

A B

-t

A

-ban, azaz

P

-ben érintő kört vesszük. Ekkor az érintő azonos az

A B

egyenessel. A másik kör viszont azonos az

A B C

háromszög köré írt körrel, így

P

-beli, más szóval

A

-beli kiszemelt félérintője

γ

szöget zár be

A B

-vel.
A kiválasztott szögre talált értékek egymás kiegészítő szögei, ezért összefoglalva kimondhatjuk, hogy a két érintő közti szögek egyike mindig

γ

Takács László (Sopron, Széchenyi I. G.)