Kezdőlap


Feladat:	983. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Babai L. , Bulkai T. , Dobozy O. , Faragó T. , Moson P. , Szeredi P. , Takács L.
Füzet:	1966/november, 138 - 142. oldal		PDF \| MathML
Témakör(ök):	Körérintési szerkesztések, Gyakorlat, Esetvizsgálat
Hivatkozás(ok):	Feladatok: 1965/április: 983. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat nem kívánta minden megfelelő körhármas megszerkesztését, itt mégis vázoljuk az összes megoldásokat, de ‐ hely hiányában ‐ a kölcsönös helyzet lehetőségeire vonatkozó megállapításaink teljes átgondolását egy-két példa mintájára az olvasóra kell bíznunk. A $k_{i}$ kör középpontját $O_{i}$ -vel, sugarát $r_{i}$ -vel jelöljük, 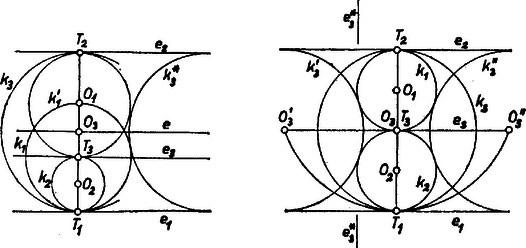$i = 1$ , $2$ , $3$ .
a) rész. Feküdjék $e_{3}$ az $e_{1}$ és $e_{2}$ között. $k_{1}$ és $k_{2}$ csak az $e_{3}$ -on tetszés szerint felvett $T_{3}$ érintési pontjukban érinthetik egymást, és $T_{3}$ -nak $e_{1}$ -en és $e_{2}$ -n levő vetületét $T_{1}$ -gyel, ill. $T_{2}$ -vel jelölve $k_{1}$ csak a $T_{3} T_{2}$ , $k_{2}$ pedig csak a $T_{3} T_{1}$ átmérő fölötti kör lehet. Ekkor a $T_{1} T_{2}$ átmérő fölötti kör megfelel $k_{3}$ -ként (l. a ábra). Ha $e_{3}$ közelebb van pl. $e_{1}$ -hez, mint $e_{2}$ -höz, akkor más megoldás nincs, hiszen amennyiben egy az $e_{1}$ -et és $e_{2}$ -t érintő $k_{3}^{*}$ kör kívülről érinti $k_{1}$ -et, akkor érinti $k_{1}$ -nek a $T_{1} T_{2}$ szakasz $e$ felező merőlegesére vett $k'_{1}$ tükörképét is, $k'_{1}$ viszont a belsejében tartalmazza $k_{2}$ -t, és érintkezési pontjuk nincs rajta a $k_{3}^{*}$ -on, tehát $k_{2}$ nem érintheti $k_{3}^{*}$ -ot.

1. a. és 1.b. ábra

Ha viszont

e_{3}

azonos

e

-vel, akkor

k_{3}

-ra nyilvánvalóan további két lehetőség van,

O'_{3}

-t és

O''_{3}

-t az

O_{1}

körüli,

O_{1} T_{1}

sugarú kör metszi ki

e_{3}

-ból (l. b ábra).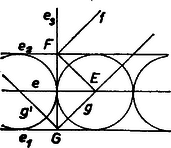

b) rész. A szerkesztéseket

r_{1}

és

r_{2}

kiszámításával készítjük elő,

r_{3}

-at véve egységnek.

O_{3}

a fenti

e

egyenesen lesz.

e_{3}

és

e

az adatok ábrájának szimmetria-tengelyei, minden megfelelő körhármasnak ezekre való tükörképe is megfelelő, megjegyezve, hogy az

e

-re való tükrözés felcseréli

e_{1}

és

e_{2}

, valamint

k_{2}

és

k_{1}

szerepét. Elég tehát azokat a megoldásokat megkeresnünk, amelyekben

O_{1}

a 2. ábra jobb fölső

e

e_{3}

derékszögtartományában van, vagyis az

f

szögfelező félegyenesen vagy az

F E

szakaszon. Nem lehet

O_{1}

F

-ben, továbbá

E

-ben sem, különben nem lehetne

k_{1}

k_{2}

és

k_{3}

három különböző kör. Így

k_{1}

-nek nem lesz pontja

e_{1}

-en, sem alatta, ezért

k_{2}

csak

e_{1}

fölött, vagyis

O_{2}

csak a

g

és

g'

félegyenesen lehet. ‐ Az

O_{1}

és

O_{2}

helyzetére megállapított

2

‐

2

lehetőséget kombinálva 4 esetet kapunk.

2. ábra

I. eset. Legyen

O_{1}

f

-en,

O_{2}

g

-n. Ekkor

k_{1}

és

k_{3}

csak kívülről érinthetik egymást

O_{1}

-nek

e_{2}

-n levő

O''_{1}

vetületében, ezért

e_{2} ⊥ O_{1} O_{3} ∥ e_{3}

(3. ábra).

k_{1}

k_{2}

-vel is csak külső érintkezésben állhat,

O_{1} O_{2} = r_{1} + r_{2}

. Belső érintkezés esetében ugyanis

O_{1}

-nek

e_{3}

-on levő

O'_{1}

vetületében érintkeznének,

O_{1} O_{2}

merőleges lenne

e_{3}

-ra,

k_{1}

k_{2}

belsejében lenne, hiszen

r_{2} = r_{1} + 2

állana fenn; ezért

k_{3}

is benne lenne

k_{2}

-ben ‐ különben nem érinthetné

k_{1}

-et ‐, ennélfogva csak az

e_{1}

-en érintkezhetnének,

O_{2} O_{3}

merőleges lenne

e_{1}

-re, azaz párhuzamos lenne

e_{3}

-mal, ez viszont nem állhatna fenn

O_{1} O_{3} ∥ e_{3}

miatt. ‐ Hasonlóan

k_{2}

és

k_{3}

is csak kívülről érintkezhetnek,

O_{2} O_{3} = r_{2} + 1.

Érintse

k_{2}

e_{3}

-at

O'_{2}

-ben,

e_{1}

-et

O''_{2}

-ben,

k_{3}

e_{1}

-et

O'_{3}

-ben, és legyen

O_{2}

vetülete az

O_{1} O'_{1}

egyenesen

O'''_{2}

. Ekkor

O_{1} O'''_{2} = | r_{1} - r_{2} |

, és az

O_{1} O_{2} O'''_{2}

derékszögű háromszögből az érintési pontok távolságára:

\begin{matrix} O'_{1} O'_{2}^{2} = O'''_{2} O_{2}^{2} = O_{2} O_{1}^{2} - O'''_{2} O_{1}^{2} = {(r_{1} + r_{2})}^{2} - {(r_{1} - r_{2})}^{2} = 4 r_{1} r_{2} . \end{matrix}

(1)

Mivel itt még

O'_{1} O'_{2} = | G O'_{1} - G O'_{2} | = | O'_{3} O_{1} - O''_{2} O_{2} | = | r_{1} + 2 - r_{2} |

, azért

\begin{matrix} {(r_{1} + 2 - r_{2})}^{2} = 4 r_{1} r_{2} . \end{matrix}

(2)

3. ábra

Másrészt (1)-ben

r_{1}

helyére

r_{3} = 1

-et írva a

k_{2}

k_{3}

kör-pár

e_{1}

-en levő érintési pontjainak távolságára kapunk egyenletet:

\begin{matrix} O'_{3} O''_{2}^{2} = 4 r_{2}, és O'_{3} O''_{2} = O_{1} O'''_{2} miatt {(r_{1} - r_{2})}^{2} = 4 r_{2} . \end{matrix}

(3)

Vonjuk ki (3)

2

-szereséből (2)-t; az egyenlet így alakítható:

\begin{matrix} {(r_{1} + r_{2})}^{2} - 4 (r_{1} + r_{2}) - 4 = 0, és innen r_{1} + r_{2} = 2 \pm 2 \sqrt[]{2} . \end{matrix}

A negatív érték azonban feladatunkban nem használható; így

r_{2} = 2 + 2 \sqrt[]{2} - r_{1}

alapján (3)-ból

\begin{matrix} r_{1}^{2} - (1 + 2 \sqrt[]{2}) r_{1} + 1 = 0, amiből \\ r_{1} = (1 + 2 \sqrt[]{2} \pm \sqrt[]{5 + 4 \sqrt[]{2}}) / 2, r_{2} = (3 + 2 \sqrt[]{2} \mp \sqrt[]{5 + 4 \sqrt[]{2}}) / 2. & (4) \end{matrix}

Mindkét megoldásban

r_{1}

és

r_{2}

pozitív, megfelelők. (A kisebb

r_{1}

esetében adódó körhármas az ábrán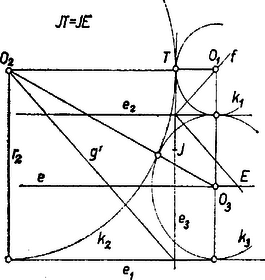

k_{1}^{*}

k_{2}^{*}

k_{3}^{*}

4. ábra

II. eset. Legyen

O_{1}

f

-en,

O_{2}

g'

-n. Ekkor

k_{1}

és

k_{2}

két oldalról érintik

e_{3}

-at,

r_{2} = r_{1} + 2

k_{2}

és

k_{3}

is kívülről érintkeznek (4. ábra). Az

O_{1} O_{2} O_{3}

derékszögű háromszögből, majd

r_{2}

-t kiküszöbölve

\begin{matrix} O_{2} O_{3}^{2} = {(r_{2} + 1)}^{2} = {(r_{2} + r_{1})}^{2} + {(r_{1} + 1)}^{2}, \\ {(r_{1} + 3)}^{2} = {(2 r_{1} + 2)}^{2} + {(r_{1} + 1)}^{2} = 5 {(r_{1} + 1)}^{2}, \\ r_{1} + 3 = \pm \sqrt[]{5} (r_{1} + 1), r_{1} = (\sqrt[]{5} - 1) / 2, r_{2} = (\sqrt[]{5} + 3) / 2. & (5) \end{matrix}

III. eset. Legyen

O_{1}

F E

szakaszon,

O_{2}

g

-n. Tekintsük először az olyan körhármasokat, amelyekben van belső érintkezés. Két ilyen helyzetű kör közül a belsőt is harmadik körünk csak úgy érintheti, ha maga is benne van a külső körben, de nincs benne a belsőben. Előírásunk szerint

r_{1} < 1 = r_{3}

, ezért

k_{1}

csak belső kör lehet.
Ha még

r_{2} < 1

, akkor

k_{2}

is a

k_{3}

-ban van. Ekkor

r_{1} = r_{2}

, mert

k_{1}

-nek

e_{2}

-n és

k_{2}

-nek

e_{1}

-en levő érintési pontját összekötő egyenes merőleges

e_{1}

-re, tehát párhuzamos

e_{3}

-mal, hiszen ezek egyben

k_{3}

érintési pontjai. Továbbá

k_{1}

és

k_{2}

külső érintkezése miatt

2 r_{1} + 2 r_{2} = 2

, és így

r_{1} = r_{2} = 1 / 2

. (Lásd az 1. ábra b) részén a

k_{1}

k_{2}

k_{3}

körhármast, ha az ottani

e_{3}

helyett a vázolt

e_{3}^{*}

egyenest vesszük. Így

k_{3}

helyett az ábra

k'_{3}

és

k''_{3}

köre is megfelelő hármast ad

k_{1}

-gyel és

k_{2}

-vel összekapcsolva. Mutassa meg az olvasó, hogy nincs más olyan megoldás, melyben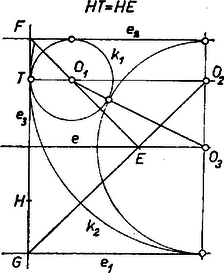

r_{1} = r_{2}

5. ábra

Ha pedig

r_{2} > 1

, akkor

k_{2}

zárja magába

k_{1}

-et és

k_{3}

-at (5. ábra). Ekkor

r_{2} = 2 - r_{1}

O_{1} O_{2} = r_{2} - r_{1} = 2 - 2 r_{1}

O_{2} O_{3} = r_{2} - 1 = 1 - r_{1}

O_{1} O_{3} = r_{1} + 1

, így az

O_{1} O_{3} O_{2}

derékszögű háromszögből

\begin{matrix} {(2 - 2 r_{1})}^{2} + {(1 - r_{1})}^{2} = 5 {(1 - r_{1})}^{2} = {(r_{1} + 1)}^{2}, \sqrt[]{5} (1 - r_{1}) = \pm (r_{1} + 1), \\ r_{1} = (3 - \sqrt[]{5}) / 2, r_{2} = (\sqrt[]{5} + 1) / 2. & (6) \end{matrix}

Mindhárom kör-pár külső érintkezése esetére már csak azokat a megoldásokat keressük, amelyekben

r_{1} \neq r_{2}

. Ekkor nincs olyan megoldás, amelyben

O_{2}

közelebb van

e_{1}

-hez, mint

O_{1}

, vagyis

r_{2} < 2 - r_{1}

. Ilyenkor ugyanis (1)-ből négyzetgyökvonással

\begin{matrix} O'_{1} O'_{2} = 2 - r_{1} - r_{2} = 2 \sqrt[]{r_{1} r_{2}}, azaz \sqrt[]{r_{1}} + \sqrt[]{r_{2}} = \sqrt[]{2} . \end{matrix}

(7)

O_{3}

nem lehet

e_{3}

-tól jobbra; legyen ezért

O_{3}

e_{3}

bal oldalán, tőle

p

távolságban. (1)-et a

k_{1}

k_{3}

és a

k_{2}

k_{3}

párra alkalmazva és négyzetgyököt vonva, majd kivonással, osztással

\begin{matrix} 2 \sqrt[]{r_{1}} = p + r_{1}, \\ 2 \sqrt[]{r_{2}} = p + r_{2}, \\ 2 (\sqrt[]{r_{2}} - \sqrt[]{r_{1}}) = r_{2} - r_{1} = (\sqrt[]{r_{2}} - \sqrt[]{r_{1}}) (\sqrt[]{r_{2}} + \sqrt[]{r_{1}}), \\ 2 = \sqrt[]{r_{2}} + \sqrt[]{r_{1}}, & (8) \end{matrix}

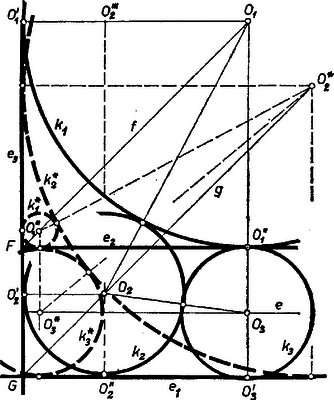
ellentétben (7)-tel. ‐ Ha viszont

O_{2}

távolabb van

e_{1}

-től, mint

O_{1}

, vagy ha távolságuk egyenlő, (7) így alakul (6. ábra):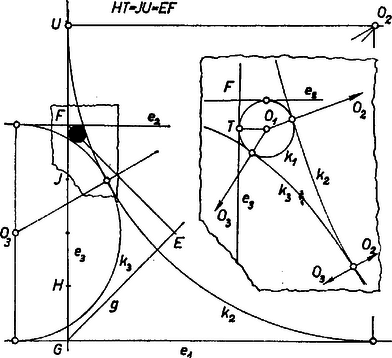

6. ábra

\begin{matrix} r_{2} - (2 - r_{1}) = 2 \sqrt[]{r_{1} r_{2}}, \\ \sqrt[]{r_{2}} - \sqrt[]{r_{1}} = \sqrt[]{2}, \end{matrix}

amit (8)-cal összekapcsolva

\begin{matrix} r_{1} = (3 - 2 \sqrt[]{2}) / 2, r_{2} = (3 + 2 \sqrt[]{2}) / 2. \end{matrix}

(9)

7. ábra

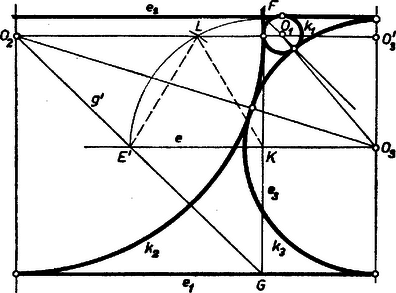IV. eset. Végül

O_{1}

-et

F E

-n,

O_{2}

-t

g'

-n keresve (7. ábra)

F E ∥ g'

miatt

O_{1} O_{2} = r_{1} + r_{2} = 2

, csak külső érintkezés lehet, így

O_{1} O_{3} = r_{1} + 1

O_{2} O_{3} = r_{2} + 1 = 3 - r_{1}

. Legyen

O_{3}

vetülete az

O_{1} O_{2}

egyenesen

O'_{3}

, ekkor

O'_{3} O_{3} = 1 - r_{1}

. Az

O_{3} O'_{3} O_{1}

és

O_{3} O'_{3} O_{2}

derékszögű háromszögből Pitagorasz tétele alapján

\begin{matrix} O'_{3} O_{1}^{2} = 4 r_{1}, O'_{3} O_{2}^{2} = 4 (2 - r_{1}) > 4 = O_{1} O_{2}^{2}, \end{matrix}

tehát

O_{1}

O_{2} O'_{3}

szakaszon van. Ezért

\begin{matrix} O_{2} O'_{3} = O_{2} O_{1} + O_{1} O'_{3} \sqrt[]{2 - r_{1}} = 1 + \sqrt[]{r_{1}}, \\ 2 r_{1} + 2 \sqrt[]{r_{1}} - 1 = 0, a pozitív gyök \sqrt[]{r_{1}} = (\sqrt[]{3} - 1) / 2, \\ r_{1} = 1 - \sqrt[]{3} / 2, r_{2} = 1 + \sqrt[]{3} / 2. & (10) \end{matrix}

Áttérve a szerkesztésre,

k_{1}

és

k_{2}

érintési pontjai a (4), (5), (6), (9) és (10) kifejezések alapján jelölhetők ki,

O_{3}

pedig

O_{1}

vagy

O_{2}

helyzete alapján. A 4‐7. ábrákon a jegyzet utal erre,

H

J

K

F G

szakasz negyedelő pontjai, így

H E = J E = \sqrt[]{5} / 2

. A (4) kifejezések harmadik tagja annak a derékszögű háromszögnek a második befogója, amelyben az átfogó

1 + 2 \sqrt[]{2}

, és az első befogó

2

.
A szimmetrikus megoldásokat is számba véve a követelményeknek

30

körhármas tesz eleget.

(Összeállítva több dolgozatból, számos kiegészítéssel.)