Kezdőlap


Feladat:	974. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Varga Gabriella
Füzet:	1966/január, 8 - 9. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Tengelyes tükrözés, Középvonal, Szögfelező egyenes, Beírt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1965/március: 974. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Messe az $A B$ egyenest a $C C_{1}$ egyenes $G_{1}$ -ben, $C C_{2}$ pedig $G_{2}$ -ben, és legyen a beírt $k$ kör érintési pontja a $B C$ oldalon $D$ , az $A B$ -n $F$ (1. ábra). Így $C$ és $G_{1}$ , továbbá $E$ és $F$ tükrös pontpár az $A C_{1}$ szögfelezőre, hasonlóan $C$ és $G_{2}$ , valamint $D$ és $F$ egymás tükörképei $B C_{2}$ -re. Ezért egyrészt $C G_{1} = 2 \cdot C C_{1}$ , $C G_{2} = 2 \cdot C C_{2}$ , tehát $C_{1} C_{2}$ , mint a $C G_{1} G_{2}$ háromszög középvonala, fele a $G_{1} G_{2}$ szakasznak. Másrészt

\begin{matrix} G_{1} G_{2} = G_{1} F + F G_{2} = C E + D C = 2 \cdot C E, \end{matrix}

mert

C D

és

C E

k

-hoz húzott érintőszakaszok, így valóban

C_{1} C_{2} = C E

.
A felhasznált

G_{1}

G_{2}

metszéspontok mindig létrejönnek, mert pl.

C C_{1}

-nek

A B

-vel bezárt (egyik) szöge

(180^{\circ} - α) / 2

, tehát

C C_{1}

nem lehet párhuzamos

A B

-vel. ‐ Továbbá

F

mindig a

G_{1} G_{2}

szakaszon van, ugyanis az

F

-nek

G_{1}

azon az oldalán van, mint a

B

csúcs,

G_{2}

pedig azon, mint

A

. Valóban,

F E

elválasztja a vele párhuzamos

G_{1} C

egyenes

C

pontját

A

-tól ‐ hiszen

E

A C

szakaszon van ‐, és hasonlóan

A

-t

B

-től. A

G_{2}

-re mondott állítás pedig a pontoknak az

F D

egyeneshez viszonyított helyzete alapján hasonlóan látható be.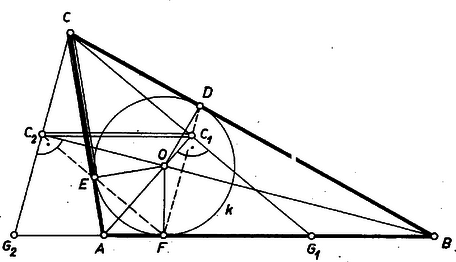

1. ábra

Megjegyzés. A

C D = C E

egyenlőségből azt is kaptuk, hogy

F

felezi a

G_{1} G_{2}

oldalt, így a

C G_{1} G_{2} ▵

-ben

F C_{2}

és

F C_{1}

is középvonalak. Ezért

F C_{1}

párhuzamos

G_{2} C

-vel, így merőleges a

B C_{2}

szögfelezőre, tehát átmegy

F

tükörképén, a

D

ponton, amit úgy is mondhatunk, hogy a

k

kör

D

F

érintési pontjait összekötő egyenes átmegy

C

-nek az

A

-ból kiinduló szögfelezőre való vetületén. Hasonlóan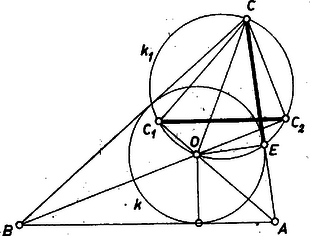

F E

átmegy

C_{2}

-n.

2. ábra

II. megoldás. A szögfelezők átmennek

k

középpontján,

O

-n, így a

C O

szakasz

C_{1}

-ből és

C_{2}

-ből derékszögben látszik, tehát

C_{1}

és

C_{2}

C O

szakasz fölötti

k_{1}

Thalész‐kör pontjai (2. ábra). Másrészt az érintés miatt

E

is a

k_{1}

-en van, így az összehasonlítandó szakaszok a

k_{1}

kör húrjai. Az állítást avval bizonyítjuk, hogy

k_{1}

-ben a két húrhoz egyenlő, ill. egymást

180^{\circ}

-ra kiegészítő kerületi szögek tartoznak.

C_{1} O C_{2} ∢

A O B ∢

csúcsszöge, vagy

180^{\circ}

-ra kiegészítő szöge (belátható volna, hogy mindig az előbbi). A háromszög szögeinek szokásos jelölésével

\begin{matrix} A O B ∢ = 180^{\circ} - (O A B ∢ + O B A ∢) = 180^{\circ} - \frac{α + β}{2} = 90^{\circ} + \frac{γ}{2} . \end{matrix}

Másrészt

C O

felezi a

γ

szöget, és így a

C E O

derékszögű háromszögből

\begin{matrix} C O E ∢ = 90^{\circ} - \frac{γ}{2} . \end{matrix}

Így

C_{1} C_{2}

-nek és

C E

-nek a

k_{1}

kör

O

pontjából vett látószöge valóban vagy egyenlő vagy egymást kiegészítő szöge. Ezt akartuk bizonyítani.

Varga Gabriella (Szombathely, Savaria g., II. o. t.)