Kezdőlap


Feladat:	967. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Palla László , Vízvári Béla
Füzet:	1965/december, 211 - 213. oldal		PDF \| MathML
Témakör(ök):	Alakzatba írt kör, Érintőnégyszögek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1965/február: 967. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Ha a négyszög mindnégy oldalegyenesének a körrel való érintkezési pontja a négyszög oldalszakaszán van, akkor a kör nyilvánvalóan a négyszög belsejében van (1. ábra), és a négyszög belső szögeinek felezői átmennek $O$ -n. Legyen az $A$ , $B$ , $C$ , $D$ csúcsnál levő szög rendre $α$ , $β$ , $γ$ , $δ$ . Így

\begin{matrix} A O B ∢ + C O D ∢ = 180^{\circ} - O A B ∢ - O B A ∢ + (180^{\circ} - O C D ∢ - O D C ∢) = \\ = 360^{\circ} - \frac{α + β + γ + δ}{2} = 180^{\circ}, \end{matrix}

mert a négyszög szögeinek összege

360^{\circ}

.
Ugyanez az érték adódik hasonló számítással a

B O C

és

D O A

szögek összegére is, vagy figyelembe vehetjük azt is, hogy a vizsgálandó négy szög összege

360^{\circ}

, így a másik két szög összege ismét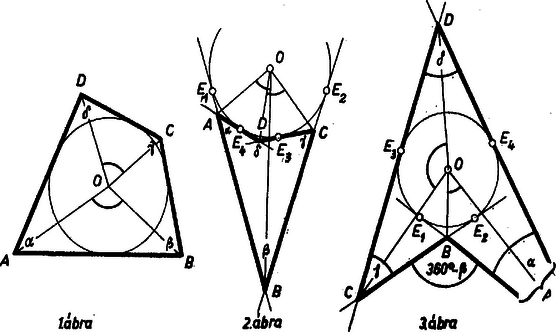

180^{\circ}

II. A második helyzettípushoz természetesen hozzáértjük, hogy a további két oldalegyenes érintési pontja oldalszakaszon van. A kört az oldalszakaszon kívüli pontjában érintő oldalegyenesek kölcsönös helyzetére két lehetőség van: a négyszög megfelelő oldalai szomszédosak (2. és 3. ábra,

A B

és

B C

), vagy szemben fekvők (4. ábra,

A B

és

C D

).
A 2. ábra esetében

A

és

C

B

-ből a körhöz húzható

B E_{1}

, ill.

B E_{2}

érintőszakaszon van, másrészt a

D

-ből húzható

D E_{4}

, ill.

D E_{3}

érintőszakasznak az érintési ponton túli meghosszabbításán, a négyszög konkáv,

D

-nél levő szöge nagyobb

180^{\circ}

-nál. Itt az

A

-ból húzható érintőszakaszok közti, a kört tartalmazó szögtartomány nagysága

180^{\circ} - α

; hasonlóan

\begin{matrix} E_{2} C E_{3} ∢ = 180^{\circ} - γ, E_{3} D E_{4} ∢ = 360^{\circ} - δ, \end{matrix}

és az

A O

C O

D O

félegyenes rendre ezeket a szögeket felezi.
A kérdéses szögek:

\begin{matrix} A O B ∢ = O A E_{1} ∢ - O B E_{1} ∢ = \frac{180^{\circ} - α - β}{2}; \\ C O D ∢ & = 180^{\circ} - (O C E_{3} ∢ + O D E_{3} ∢) = 180^{\circ} - (\frac{180^{\circ} - γ + 360^{\circ} - δ}{2}) = \\ = \frac{γ + δ}{2} - 90^{\circ}, \end{matrix}

összegük

γ + δ - 180^{\circ}

, másképpen

180^{\circ} - α - β

, ugyanis konkáv négyszögre is fennáll

α + β + γ + δ = 360^{\circ}

. Továbbá hasonlóan

\begin{matrix} B O C ∢ + D O A ∢ = 180^{\circ} - β - γ = α + δ - 180^{\circ} . \end{matrix}

A 3. ábra csak abban tér el a 2.-tól, hogy

B

van az

A E_{1}

és

C E_{2}

érintőszakaszon, a négyszög konkáv szöge

B

-nél van. Így

\begin{matrix} A O B ∢ + C O D ∢ & = (180^{\circ} - \frac{α}{2} - \frac{β}{2}) + (180^{\circ} - \frac{γ}{2} - \frac{δ}{2}) = \\ = 180^{\circ} = B O C ∢ + D O C ∢ . \end{matrix}

A 4. ábrán a feltevés hurkolt négyszöget eredményez. Ezzel az esettel nem foglalkozunk, mert már a négyszög szögeinek értelme is bizonytalanná válik itt.
III. Az utolsó vizsgálandó helyzettípusban, az 5. ábra esetében a kört tartalmazó szögtartomány a

B

csúcsban maga a

β

szögtartomány,

D

-ben a

δ

szög csúcsszögtartománya,

A

-ban és

C

-ben pedig

α

, ill.

γ

mellékszögtartománya. Így

\begin{matrix} A O B ∢ + C O D ∢ & = (O A E_{1} ∢ - O B E_{1} ∢) + (O D E_{3} ∢ - O C E_{3} ∢) = \\ = 180^{\circ} - α - β, \\ B O C ∢ + D O A ∢ & = (O C E_{2} ∢ - O B E_{2} ∢) + (O D E_{4} ∢ - O A E_{4} ∢) = \\ = 180^{\circ} - β - γ . \end{matrix}

Palla László (Budapest, Piarista g. II. o. t.)

Vízvári Béla (Budapest, Berzsenyi D. g. II. o. t.)

Megjegyzés. A feladattal a szerkesztőség arra kívánta ráirányítani az olvasók figyelmét, hogy a helyzet megváltozásával tételek kissé módosulhatnak, másrészt hogy egy négyszög mindegyik oldalegyenesét érintő kör lehet a négyszögön kívül is a háromszög esetéhez hasonlóan.
Az eredményeket egybevetve mondhatjuk, hogy ha a kör a négyszög belsejében van (1. és 3. ábra), akkor a kérdéses összegek egyenlők. Másrészt a 2. és 5. ábra helyzeteiben a két összegre ugyanaz a kifejezés adódott. Ezekben a helyzetekben észre lehetett volna venni az előbbi szép összefüggés helyébe azt, hogy

A O B ∢ - C O D ∢

és

B O C ∢ - D O A ∢

különbségek egyenlők, közös értékük

0^{\circ}

, vagyis

A O B ∢ = C O D ∢

, és

B O C ∢ = D O A ∢

. Ennek bizonyítását az olvasóra hagyjuk.
Ajánljuk azt is az olvasóknak, vizsgálják meg a teljesség kedvéért, hogy ábráink feltüntetnek-e minden lehetséges helyzettípust.