Feladat: 958. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Ambrus G. ,  Antos P. ,  Babai L. ,  Balázs Katalin ,  Bulkai T. ,  Eszes G. ,  Farkas Ágnes ,  Feldusz M. ,  Grósz T. ,  Halász F. ,  Havas J. ,  Kugler S. ,  Laborci Z. ,  Marossy F. ,  Mérő L. ,  Nagy Béla ,  Pataki Judit ,  Péli Katalin ,  Rajczy P. ,  rátky Gy. ,  Sas Éva ,  Szabados Katalin ,  Szeredi P. ,  Szikora J. ,  Szolga B. ,  Szűcs A. ,  Tátray P. ,  Tegze Judit ,  Újvári István ,  Verbényi Márta 
Füzet: 1965/október, 58 - 59. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Pont, Téglalapok, Deltoidok, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat
Hivatkozás(ok):Feladatok: 1965/január: 958. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. a) Az E, F, G pontok szerkesztésekor keletkező merőleges szárú szögek, ill. a szögfelezés révén következik ‐ amennyiben megmutatjuk, hogy a fellépő szögek hegyesszögek ‐, hogy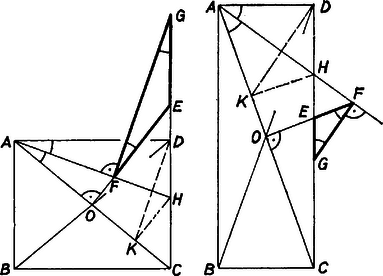

EGF∢=DAF∢=FAC∢=GFE∢,
s így az EFG háromszög egyenlő szárú.
 
 

A négy szög közül a középső kettő hegyesszög fele, s így hegyesszög. A másik kettő hegyesszög voltához azt mutatjuk meg, hogy FEG tompaszög, éspedig az OCE derékszögű háromszög OEC hegyesszögének kiegészítő szöge. Jelöljük AF és CD metszéspontját H-val. Ha F az ACD háromszögben van, akkor OFH és CHF tompaszög, mert mindkettő hegyesszög mellékszöge, így E a CH egyenes H-n túli és OF-nek az F-en túli meghosszabbításán van. Ugyancsak CHF tompaszög volta miatt, és mert GF merőleges AH-ra, G is a CH H-n túli meghosszabbításán van. Mivel GFH∢=90∘, és EFH∢, mint AFO∢ csúcsszöge, hegyesszög, így FE a GFH derékszögű szögtartományban halad, tehát a C, H, E, G pontok ebben a sorrendben következnek, FEG∢ tehát az FEC∢ mellékszöge.
Ha F az ACD háromszögön kívül, tehát AH-nak a H-n túli meghosszabbításán van, akkor az ACH háromszög AC oldalszakaszát és az AH oldal meghosszabbítását metsző OF egyenes metszi a CH oldalszakaszt. Másrészt CHF∢=DHA∢ hegyesszög, így az AF-re állított FG merőleges is a H-ból C felé menő félegyenest metszi, és mivel AFO hegyesszög, FE(=FO) a derékszögű AFG szögtartományban halad. Így E most is G és H közt van, tehát FEG a CEO szög mellékszöge. Ezzel a bizonyítást befejeztük.
b) Ha F egybeesik E-vel, akkor AF=AE=EC, s így DAE∢=CAE∢=ACE∢; másrészt e három szög összege 90∘, így mindegyik 30∘-os és DAC∢=60∘. Ebben az esetben az EFG△ elfajul ponttá.
 
 Szabados Katalin (Budapest, Berzsenyi D. g. I. o. t.)
 

II. megoldás. a) Jelöljük AF és CD metszéspontját H-val, H-ból az AC-re bocsátott merőleges talppontját K-val. Ekkor DHK egyenlő szárú háromszög, mert H, mint a szögfelező pontja, egyenlő távolságra van a szög két szárától: HD=HK. Ekkor ADHK deltoid, AH és KD átlói merőlegesek. Így HK∥EF, KD∥FG (merőlegesek AC-re, ill. AF-re) és DH∥GE (egy egyenesen vannak). Az EFG△ oldalai tehát párhuzamosak a HKD△ megfelelő oldalaival, s így a két háromszög hasonló, tehát az EFG△ is egyenlő szárú.
b) E és F akkor és csak akkor esik egybe, ha K és O egybeesik. Ekkor KD a BD átló fele, s így ADHK deltoid volta miatt KD=KA=AD, tehát ADK szabályos háromszög, DAC∢=DAK∢=60∘.
 

Megjegyzés. A b) kérdés tárgyalható számítás útján is Pythagoras tétele és a szögfelezőre vonatkozó osztásarány-tétel felhasználásával.
Legyen CD=a, DA=b, AC=c. Az EOC és ADC△-ek hasonlóságából CE=c2/2a. Az osztás-arányból CF=AC⋅CD/(AD+AC)=ac/(b+c). Egyenlőségükből
c(b+c)=2a2=2c2-2b2=(2c-2b)(b+c),
így c=2b, ADC egy szabályos háromszög fele, DAC∢=60∘.