Kezdőlap


Feladat:	951. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bod Judit , Csirmaz L. , Gáspár A. , Hunyadvári L. , Kele A. , Kovács M. , Laborczi Z. , Lukács G. , Szalay S. , Szeredi P. , Tuba Mária
Füzet:	1966/március, 115. oldal		PDF \| MathML
Témakör(ök):	Alakzatok szimmetriái, Tengelyes tükrözés, Pont körüli forgatás, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/december: 951. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Ha egy idomnak $t_{1}$ és $t_{2}$ szimmetriatengelye, akkor $t_{2}$ -nek $t_{1}$ -re vonatkozó $t_{2}^{*}$ tükörképe is szimmetriatengelye, hiszen szimmetriatengelye a $t_{1}$ -re vonatkozó tükörképnek, de ez azonos az eredeti idommal, mert $t_{1}$ szimmetriatengely.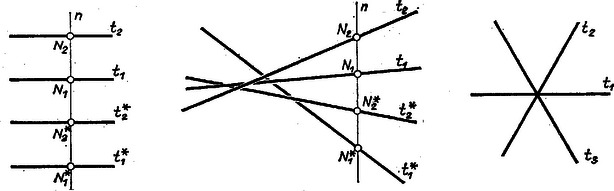

II. A feladat feltételei mellett a tengelyek páronként metszik egymást. Valóban, ha volna két párhuzamos vagy két kitérő tengely,

t_{1}

és

t_{2}

, akkor messe ezeket egy rájuk merőleges egyenes, ill. normáltranzverzálisuk,

n

N_{1}

és

N_{2}

pontban (

a - b

ábra). Ekkor

t_{2}

-nek

t_{1}

-re vonatkozó

t_{2}^{*}

tükörképe metszi

n

-et

N_{2}

-nek

N_{1}

-re vonatkozó

N_{2}^{*}

tükörképében, tehát

N_{1}

nek az

N_{2}

-t nem tartalmazó oldalán. Hasonlóan

t_{1}

-nek

t_{2}^{*}

-ra vonatkozó

t_{1}^{*}

tükörképe

n

-t az

N_{1}

-nek

N_{2}^{*}

-ra vonatkozó

N_{1}^{*}

tükörképében metszi, tehát

N_{2}^{*}

-nak az

N_{1}

-et és

N_{2}

-t nem tartalmazó oldalán. Így

t_{1}

t_{2}

t_{1}^{*}

t_{2}^{*}

négy különböző egyenes, és I. szerint mind szimmetriatengelye volna az idomnak, holott a feltétel szerint annak csak 3 szimmetriatengelye van. (Az eljárás ismétlése végtelen sok szimmetriatengelyt szolgáltatna.)

III. A 3 tengely nem lehet páronként merőleges, mert ha pl.

t_{1}

és

t_{2}

merőleges

t_{3}

-ra, akkor vagy párhuzamosak, vagy kitérők, de éppen beláttuk, hogy ez lehetetlen. Legyen

t_{1}

és

t_{2}

szöge

90^{\circ}

-tól különböző. Ekkor

t_{2}

-nek

t_{1}

-re vonatkozó tükörképe különbözik mindkettőjüktől, tehát csak

t_{3}

lehet. Így

t_{3}

is átmegy

t_{1}

és

t_{2}

metszéspontján;

t_{1}

-nek

t_{3}

-ra vonatkozó tükörképe pedig újra

t_{2}

(

c

ábra). Ez azt jelenti, hogy

t_{2}

-t a

(t_{2} t_{1}) ∢

-gel háromszor ugyanabban az irányban elforgatva sorra

t_{1}

-re,

t_{3}

-ra, majd újra

t_{2}

-re kerül. Ez a szög tehát

60^{\circ}

vagy

120^{\circ}

, de a két tengely közti kisebb szög az utóbbi esetben is

60^{\circ}

, és ez egyben bármelyik két tengely kisebbik szöge. Ezzel a feladat állítását bebizonyítottuk.

Tuba Mária (Gyömrő, Ált. g. I. o. t.) dolgozata, kiegészítéssel