| Feladat: | 944. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Ambrus G. , Bod Judit , Bozóky-Szeszich Á. , Dékány I. , Dobozy O. , Gáspár A. , Havas I. , Holló Cs. , Horváth S. , Kloknicer I. , Major Péter , Márkus A. , Palla L. , Say I. , Szalay Marianne , Tarján T. , Thomka I. , Varga Gabriella , Várhegyi T. , Verdes S. , Vizvári B. | ||
| Füzet: | 1965/október, 49 - 50. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkidomok átdarabolása, Diofantikus egyenletek, Kombinatorikai leszámolási problémák, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1964/november: 944. matematika gyakorlat | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A kívánt átdarabolás lehetséges, mert az adott és négyzetek területének összegével egyenlő területű négyzet oldalának hossza egész szám: (egységünk mindig a cm), ugyanis 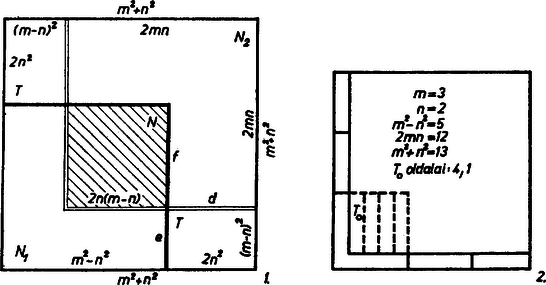 Nyilvánvaló azonban, hogy és egyikét egészben is beilleszthetjük -ba, és várható, hogy másikukat sem kell mindig ennyire felaprózni. -et és -t két szemben fekvő sarkába beillesztve egy részét kétszer fedtük le (1. ábra), mert és oldalainak összege nagyobb oldalánál, hiszen nyilván , így pedig és oldalainak különbsége, , kisebb 2 -nél, oldalánál. A kétszer fedett rész négyzet alakú, és oldala . Másrészt -ból két egybevágó téglalap fedetlen maradt, oldalaik , ill. és oldalainak különbsége: . Kivágva mármost az -et másodszor fedő részt és valamelyikéből, ezt úgy kell feldarabolnunk, hogy részeivel a -ket lefedhessük. -nek és -nek közös osztója az , oldalpárnak pedig . Ezért és felosztható olyan egybevágó téglalapokra, amelyeknek oldala és . Így szétdarabolva -et, kívánt lefedése mindenesetre végrehajtható. A idomok -ben az egyik oldaliránnyal párhuzamosan , a másikkal párhuzamosan sávot alkotnak, így számuk ; -ben viszont , ill. a sávok száma, tehát a idomok száma valóban fele az -belinek. Az -beli -ok száma annyi, mint ha -et 1 cm-es csíkokra vagdaltuk volna, de így mégsem az egész -et és -t vagdaltuk csíkokra. 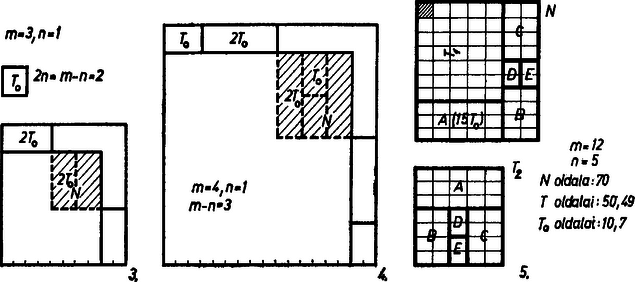 Van is olyan eset, amikor a feladat nem hajtható végre kevesebb részre vágással, mégpedig ha , mert ekkor majdnem kitölti -at, csupán egy 1 cm széles, -alakú sávot hagy fedetlenül (2. ábra, , esete). A másik véglet esetében azonban ‐ ti. amikor tölti ki majdnem -at, amikor ‐ már csökkenthető a részek száma. Ekkor -ben az egyik irányban 2 sáv van, a másik irányú sávok két-két -ját egyben hagyhatjuk, legfeljebb egyet kell kettévágni, ha ti. az különbség páratlan szám (3. és 4. ábra, , ill. 4). Ha sávjainak száma mindkét irányban nagyobb, akkor nagyobb számú is maradhat egy-egy darabban (5. ábra, , , az oldalak 119, 120, 169, ill. 70, csak feldarabolását és a második összeállítását rajzoltuk meg, részeinek száma csupán 6). Eljárásunk nem jelenti annak bizonyítását, hogy az átdarabolás nem hajtható végre kisebb számú darabra osztással. |