Feladat:	920. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Erdődy Gabriella ,  Sarkadi Nagy István
Füzet:	1965/április, 155 - 156. oldal		PDF  |  MathML
Témakör(ök):	Középponti és kerületi szögek, Kör (és részhalmaza), mint mértani hely, Húrnégyszögek, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/május: 920. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.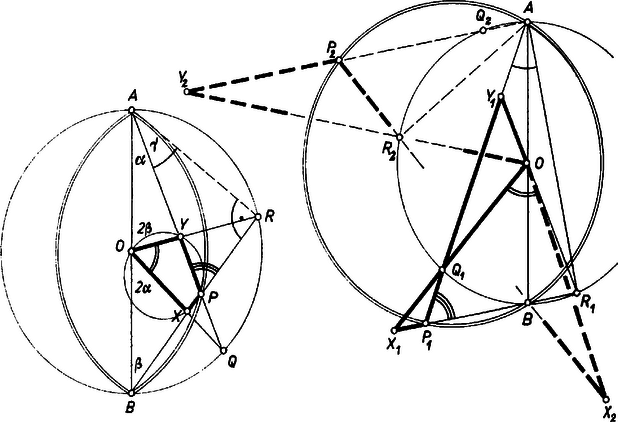     Fejezzük ki az $OXPY$ négyszög $O$-nál és $P$-nél levő szögét az $APB$ háromszög $A$-nál és $B$-nél levő $\alpha$, ill. $\beta$ szögével. Felhasználva a kerületi és középponti szögek közti összefüggést is, ${\displaystyle \begin{array}{cc}\hfill {\displaystyle XOY\sphericalangle }& {\displaystyle =QOR\sphericalangle ={180}^{\circ }-BOQ\sphericalangle -ROA\sphericalangle =}\hfill \\ \hfill {\displaystyle }& {\displaystyle ={180}^{\circ }-2\left(BAQ\sphericalangle +RBA\sphericalangle \right)={180}^{\circ }-2\left(\alpha +\beta \right);}\hfill \\ \hfill {\displaystyle XPY\sphericalangle }& {\displaystyle =BPA\sphericalangle ={180}^{\circ }-\left(\alpha +\beta \right)\mathrm{.}}\hfill \end{array}}$ Így, ha a négyszög húrnégyszög, akkor $\begin{array}{c}{\displaystyle XOY\sphericalangle +XPY\sphericalangle ={360}^{\circ }-3\left(\alpha +\beta \right)={180}^{\circ }\mathrm{,}}\end{array}$ (1) azaz $\alpha +\beta ={60}^{\circ }$, és $APB\sphericalangle ={120}^{\circ }$; megfordítva, ha ez a szögösszefüggés fennáll, akkor (1) is. Eszerint a keresett mértani hely annak a két körívnek a kör belsejébe eső pontjaiból áll, amelyekről az $AB$ átmérő ${120}^{\circ }$ alatt látszik, vagyis ebből a két körívből, a végpontjaik kivételével.    Erdődy Gabriella (Budapest, XI., Villányi úti ált. isk. 8. o. t.)   Megjegyzések. 1. Valamivel még egyszerűsödik a számítás, ha a rövidebb $QR$ íven nyugvó  $\gamma$ kerületi szöggel fejezzük ki az $O$-nál és $P$-nél keletkező szöget: $XOY\sphericalangle =QOR\sphericalangle =2\gamma$, $XPY\sphericalangle =BPA\sphericalangle =BRA\sphericalangle +QAR\sphericalangle ={90}^{\circ }+\gamma$, mint az $APR$ háromszög külső szöge; $OXPY$ pedig akkor és csak akkor húrnégyszög, ha $\gamma ={30}^{\circ }$, azaz $APB\sphericalangle ={120}^{\circ }$.    Sarkadi Nagy István (Debrecen, Ref. Koll. g. II. o. t.)   2. Ha a körön kívüli $P$ pontokat is megengedünk, ilyenekre $O$, $P$, $X$ és $Y$ akkor és csak akkor fekszik egy körön, ha $QOR\sphericalangle =2\gamma =APB\sphericalangle ={90}^{\circ }-\gamma$, amiből $APB\sphericalangle ={60}^{\circ }$ adódik. Ezek a pontok tehát a föntebb talált köríveket teljes körré kiegészítő íveket alkotják, kiveendő azonban a külső ívek felezőpontja, mert $P$-t ott véve $X$ is $Y$ nem jön létre.