Kezdőlap


Feladat:	916. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Aczél G. , Babai L. , Balogh K. , Bárány I. , Baranyai Zs. , Bódi Z. , Cziffra A. , Deák J. , Dobozy O. , Domokos Zsuzsanna , Faragó T. , Ferenczi Gy. , Ferenczi M. , Fodor Magdolna , Gáspár A. , Gyenes G. , Karsai Kornélia , Kelemen G. , Kiss Katalin , Külvári I. , Lamm P. , Loparits Éva , Major P. (Bp. Fazekas g.) , Malina J. , Márki L. , Mátrai M. , Nagy Júlia , Nagy Klára , Patkós A. , Siket Aranka , Simonovits András , Surányi L. , Szeidl L. , Székely G. , Szentiványi B. , Treer Mária
Füzet:	1965/január, 24 - 25. oldal		PDF \| MathML
Témakör(ök):	Elsőfokú (és arra visszavezethető) egyenletrendszerek, Számelrendezések, Kombinatorikai leszámolási problémák, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/május: 916. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek egy megfelelő elrendezésben a kis körökbe beírt számok $k_{1}$ , $k_{2}$ , $k_{3}$ , $k_{4}$ , az első kettő a két nagy körrel átmetszett kis körökön, éspedig $k_{1}$ a harmadik nagy kör közepén levő köröcskében, az utóbbi kettő pedig a $k_{1}$ körüli nagy kör egyszer átmetszett kis köreiben. Legyenek hasonlóan a négyzetekbe és a hatszögekbe beírt számok az 1. ábra szerint $n_{1}$ , $n_{2}$ , $n_{3}$ , $n_{4}$ , ill. $h_{1}$ , $h_{2}$ , $h_{3}$ , $h_{4}$ . Az elrendezés első követelménye szerint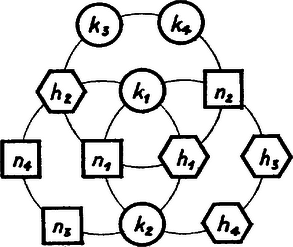

\begin{matrix} (k_{1} + k_{2} + k_{3} + k_{4}) + (n_{1} + n_{2} + n_{3} + n_{4}) + (h_{1} + h_{2} + h_{3} + h_{4}) = 78, \end{matrix}

ugyanis az első 12 természetes szám összege 78. Az egyes zárójelekben álló összegeknek a harmadik követelmény szerint egyenlőknek kell lenniük, így mindegyikben 26 az összeg. Végül a nagy körökre előírt követelmény miatt

\begin{matrix} (k_{1} + k_{2}) + (n_{1} + n_{2}) + (h_{3} + h_{4}) & = 33, \\ (k_{1} + k_{2}) + (h_{1} + h_{2}) + (n_{3} + n_{4}) & = 33, \\ (n_{1} + n_{2}) + (h_{1} + h_{2}) + (k_{3} + k_{4}) & = 33. \end{matrix}

1. ábra

Itt az első két egyenletet összeadva, a fentebbiek figyelembevételével

\begin{matrix} 2 (k_{1} + k_{2}) + 2 \cdot 26 = 66, k_{1} + k_{2} = 7, k_{3} + k_{4} = 19. \end{matrix}

Hasonlóan adódik az első és harmadik, ill. az utolsó két egyenlet összeadásával, hogy a négyzetekben és a hatszögekben is az 1-es és 2-es indexű számok összege 7, a 3-as és 4-es indexűek összege 19.
Az előírt számokból választott két különböző szám összege gyanánt 7-et is, 19-et is 3-féleképpen állíthatjuk elő:

\begin{matrix} I. & II. & III. \\ a) & 7 = 1 + 6 & = 2 + 5 = & 3 + 4, \\ b) & 19 = 7 + 12 & = 8 + 11 = & 9 + 10, \end{matrix}

ezért az elrendezés lehetséges, pl. a 2. ábrán látható módon.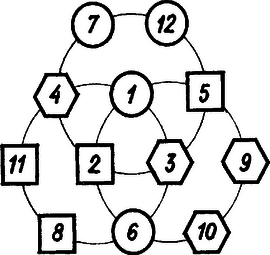

2. ábra

k_{1}

helyébe 1-től 6-ig bármelyik számot írhatjuk; ha ezt megválasztottuk,

k_{2}

helyébe

7 - k_{1}

-et kell írni. A maradó 4 szám bármelyike választható

n_{1}

-nek,

n_{2}

ezután

7 - n_{1}

lesz, végül a maradó 2 szám valamelyike

h_{1}

, a másik

h_{2}

. Így e 6 betű helyébe

6 \cdot 4 \cdot 2 = 48

-féle módon írhatunk megfelelő számokat.
Ugyanígy látható, hogy bárhogy írtunk számokat a nagy körök metszéspontjánál levő helyekre, a másik 6 helyre ismét 48-féleképpen írhatjuk a 7-tő1 12-ig terjedő egész számokat. A 12 mezőt így

48 \cdot 48 = 2304

-féleképpen tölthetjük ki.

Karsai Kornélia (Szeged, Radnóti M. G.. II. o. t.)