Kezdőlap


Feladat:	914. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Antal T. , Bálint Z. , Balogh K. , Bárány I. , Baranyai Zs. , Bóta Károly , Cziffra A. , Deák J. , Domokos L. , Domokos Zsuzsanna , Fodor Magdolna , Fűrész J. , Gloviczki P. , Gömböcz L. , Halász F. , Havas J. , Herényi I. , Horváth B. , Kafka P. , Karsai Kornélia , Kerényi L. , Kertész M. , Király L. , Kiss Á. , Kottra G. , Laborczi Z. , Lamm P. , Lelkes A. , Lévai F. , Major P. (Bp. Fazekas g.) , Malina J. , Surányi L. , Szeidl L. , Szentiványi Béla , Tihanyi Klára , Tihanyi L. , Turmezey T. , Varjas A. , Varsányi Anikó
Füzet:	1965/április, 153 - 154. oldal		PDF \| MathML
Témakör(ök):	Tengelyes tükrözés, Magasságvonal, Szögfelező egyenes, Párhuzamos szelők tétele és megfordítása, Síkgeometriai számítások trigonometria nélkül háromszögekben, Háromszögek szerkesztése, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/április: 914. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a kívánt háromszög $A B C$ , ebben a $B C = a$ oldal, valamint az $A$ csúcsból húzott $A A' = f_{a}$ szögfelező és $A A_{0} = m_{a}$ magasság rendre egyenlő az adott három hosszúsággal. Legyen továbbá az $A$ , $B$ , $C$ csúcsnál levő szög rendre $α$ , $β$ , $γ$ .

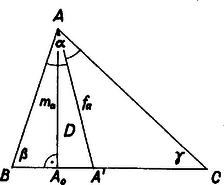1. ábra

Egyelőre feltesszük, hogy

f_{a} > m_{a}

. Így az

A A' A_{0} = D

derékszögű háromszögnek három független alkatrészét ismerjük. Szögeit kifejezhetjük az

A B C Δ

szögeivel. A feltevés miatt az

A B

és

A C

oldalak hossza különböző, válasszuk a jelölést úgy, hogy

A B < A C

, így

γ < β

. Ekkor

A'

A_{0} C

szakaszon van, és

A A' A_{0} ∢ = γ + α / 2 = [180^{\circ} - (β - γ)] / 2

, mint az

A A' C Δ

külső szöge, továbbá

\begin{matrix} A' A A_{0} ∢ = 90^{\circ} - A A' A_{0} = \frac{1}{2} (β - γ) . \end{matrix}

Eszerint

D

megszerkesztésével ismertté vált az

a

oldal végpontjainál levő szögek különbsége, ill. a kiegészítő szögének a fele, és ezzel az észrevétellel feladatunkat visszavezettük az 1964. évi Arany Dániel kezdők versenye II. fordulójának 2. feladatára^{$^{*}$} ahol éppen a szóban forgó különbség került felhasználásra. ‐ Mint láttuk, a feladatnak mindig van megoldása éspedig lényegében egy.

f_{a} = m_{a}

esetén az

A B C D Δ

szükségképpen egyenlő szárú, a szerkesztés alapfeladatnak tekinthető;

f_{a} < m_{a}

esetén pedig nincs megoldás.

Varsányi Anikó (Budapest, Ságvári E. gyak. g. I. o. t.)

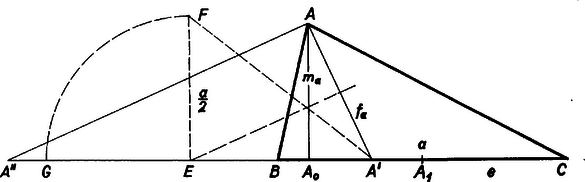2. ábra

II. megoldás. Állítsunk merőlegest az I. megoldásbeli

A A'

szögfelezőre

A

-ban, messe ez az

A' A_{0}

egyenest

A''

-ben.

A A''

A B C Δ A

-nál levő külső szögének felezője,

A''

B C

oldal

B

-n túli meghosszabbításán adódik. Ismeretes, hogy a belső szögfelező

A'

talppontja

B

-től és

C

-től mért távolságainak aránya egyenlő az

A B : A C

aránnyal, és hasonlóan belátható, hogy a tétel

A''

-re is igaz. Így

\begin{matrix} \frac{B A'}{C A'} = \frac{B A}{C A} = \frac{B A''}{C A''}, B A' \cdot C A'' = B A'' \cdot C A' . \end{matrix}

(1)

Ennek alapján kiszámíthatjuk és megszerkeszthetjük a

B A' = x

szakaszt. Ugyanis

C A' = a - x

B A'' = A' A'' - x

C A'' = C B + B A'' = a + A' A'' - x

, és itt

A' A''

kifejezhető az adatokkal: szerkesztésünk folytán az

A' A'' A

és

A' A A_{0}

derékszögű háromszögekből

\begin{matrix} A' A'' = d = \frac{A' A^{2}}{A' A_{0}} = \frac{f_{a}^{2}}{\sqrt[]{f_{a}^{2} - m_{a}^{2}}} . \end{matrix}

Mindezeket (1)-be helyettesítve a szokásos rendezési lépésekkel

\begin{matrix} x^{2} - (a + d) x + a d / 2 = 0, \\ x = x_{1} = \frac{1}{2} (a + d - \sqrt[]{a^{2} + d^{2}}) = \frac{a}{2} + \frac{d}{2} - \sqrt[]{{(\frac{a}{2})}^{2} + {(\frac{d}{2})}^{2}}, \end{matrix}

ugyanis az egyenlet

a

-nál kisebb gyökére van szükségünk. (

x_{2}

C A''

szakasz hosszát adja, ugyanis a gyökök összege

a + d

, és így

x_{2} = a + (d - x_{1}) = C B + B A'' = C A''

.)
A fentiekből a következő szerkesztés adódik. Egy

e

egyenes

A_{0}

pontjában állított merőlegesre felmérjük az adott

m_{a}

magasságot, a végpont

A

: körívet írunk

A

körül a szögfelező

f_{a}

hosszával, mint sugárral, ennek

e

-vel való egyik metszéspontja

A'

. Megszerkesztjük

A A'

felező merőlegesét, ennek

e

-vel való metszéspontja

E

. Itt merőlegest állítunk

e

-re és rámérjük az adott

a

oldal felét, úgyszintén

A' E

-nek

E

-n túli meghosszabbítására is, a végpont

F

, ill.

G

. Az

A' F

szakaszt

G

-ből

E

felé felmérve kapjuk

B

-t, és innen tovább

a

-t felmérve

C

-t.
Hely hiányában az olvasóra bízzuk a szerkesztés helyességének bizonyítását, ‐ ami csupán annak megmutatásában áll, hogy

A A'

felezi a

B A C

szöget ‐, továbbá azét, hogy

f_{a} > m_{a}

esetén mindig egy megoldás van.
Szentiványi Béla (Budapest, Rákóczi F. g. II. o. t.)

Megjegyzés. Az

A'

és

A''

pontok

B

-től mért távolsága az osztásarányra idézett tételek alapján kifejezhető az oldalakkal:

A' B = a c / (b + c)

A'' B = a c / (b - c)

. Ezekkel kifejezhetjük a

B C

oldal

A_{1}

felezőpontjától mért

A' A_{1} A'' A_{1}

távolságokat is:

A' A_{1} = A_{1} B - A' B = a (b - c) / (2 (b + c))

A'' A_{1} = A'' B + B A_{1} = a (b + c) / (2 (b - c))

, ebből az

A_{1} A' \cdot A_{1} A'' = {B C}^{2} / 4

összefüggés adódik. Ennek alapján

A_{1}

helyzetét határozhatjuk meg

A'

-höz és

A''

-höz képest a fenti eljáráshoz hasonlóan.
Bóta Károly (Budapest, Fazekas M. g. II. o. t.)

^{$^{*}$}A megoldást lásd K.M. L. 30 (1965) 2 ‐ 3. o.,