Kezdőlap


Feladat:	906. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Arányi P. , Babai László , Bárány I. , Berényi J. , Berkes István , Bóta Károly , Darvas György , Deák J. , Domokos László , Domokos Zsuzsanna , Fodor Magdolna , Gy. Molnár Csaba , Gömböcz L. , Havas János , Herényi István , Herszényi B. , Horváth Béla , Joó Piroska , Kálmán A. , Karsai Kornélia , Király L. , Kiss Ambrus , Kloknicer I. , Laborczi Zoltán , Laczkovich M. , Lamm P. , Lelkes I. , Lévai Ferenc , Lippner Gy. , Lipták J. , Major P. (Bp. Bláthy) , Major P. (Bp. Fazekas g.) , Malina János , Sarkadi Nagy István , Soltész P. , Staub Klára , Surányi László , Szász András , Szentiványi B. , Tényi G. , Tihanyi László , Tolnay-Knefély T. , Vesztergombi Katalin , Zeisler J.
Füzet:	1964/december, 216 - 218. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Középvonal, Súlyvonal, Pitagoraszi számhármasok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/március: 906. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A bizonyítandó egyenlőség bal oldalán $A E$ , $B F$ és $C G$ az $A B C$ alaplap súlyvonalai, a jobb oldalon $D E$ , $D F$ és $D G$ az oldallap-háromszögeknek a $D$ főcsúcsból kiinduló súlyvonalai.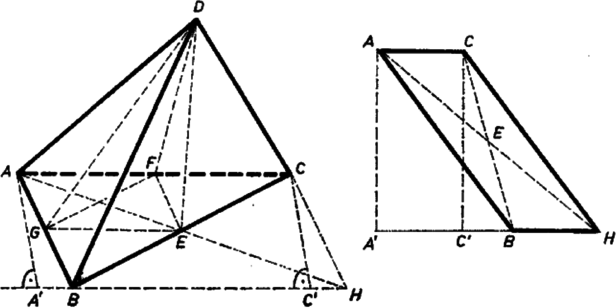

A háromszög súlyvonalai kifejezhetők az oldalakkal. Válasszuk a betűzést úgy, hogy

B A C

hegyesszög legyen, tükrözzük

A

-t

E

-re, legyen a tükörkép

H

, végül legyen

A

és

C

vetülete a

B H

egyenesen

A'

C'

. Így az

A B H C

négyszög paralelogramma,

A E = A H / 2

, és Pythagorász tételét alkalmazva egymás után az

A H A'

C B C'

A B A'

és

C H C'

derékszögű háromszögekre, valamint figyelembe véve az

\begin{matrix} A' H = A' B + B H, C' B = | B H - C' H |, A' B = C' H, \\ B H = A C és C H = A B \end{matrix}

egyenlőségeket:

\begin{matrix} A H^{2} + B C^{2} & = A A'^{2} + A' H^{2} + C' B^{2} + C C'^{2} = A A'^{2} + A' B^{2} + \\ + 2 A' B \cdot B H + B H^{2} + C' H^{2} - 2 C' H \cdot B H + B H^{2} + C C'^{2} = \\ = A B^{2} + B H^{2} + H C^{2} + C A^{2} = 2 A B^{2} + 2 A C^{2}, & (2) \end{matrix}

és így

\begin{matrix} A E^{2} = \frac{A H^{2}}{4} = \frac{1}{4} (2 A B^{2} + 2 A C^{2} - B C^{2}) . \end{matrix}

(3)

Hasonló meggondolással ugyanerre az eredményre jutunk akkor is, ha a

B A C

szög tompaszög, vagy ha derékszög; eszerint a háromszög egy súlyvonalának négyzete egyenlő a súlyvonallal közös végpontú oldalak négyzetösszege 2-szereséből, valamint a szemben fekvő oldal négyzetéből képezett különbség 4-ed részével.
Ezek szerint előbb az (1) bal oldalán, majd a jobb oldalán szereplő súlyvonalak négyzetösszege

\begin{matrix} A E^{2} + B F^{2} + C G^{2} = \frac{3}{4} (A B^{2} + B C^{2} + C A^{2}), & (4) \\ D E^{2} + D F^{2} + D G^{2} = D A^{2} + D B^{2} + D C^{2} - \frac{1}{4} (A B^{2} + B C^{2} + C A^{2}) . & (5) \end{matrix}

(1) jobb oldalán

E F

F G

G E

A B C

alapháromszög középvonalai, rendre egyenlők a háromszög oldalainak felével, így négyzetösszegük 4-szerese egyenlő az

A B C

háromszög oldalainak négyzetösszegével. Ezt (4) és (5) eredményeinkkel egybevetve kapjuk, hogy a bizonyítandó egyenlőség fennáll, mert két oldalának közös értéke:

\begin{matrix} (D A^{2} + D B^{2} + D C^{2}) + \frac{3}{4} (A B^{2} + B C^{2} + C A^{2}) . \end{matrix}

Gy. Molnár Csaba (Miskolc, Bláthy O. vill. ip. t. I. o. t.)

Megjegyzés. A (2) eredmény szerint paralelogramma átlóinak négyzetösszege egyenlő az oldalak négyzetösszegével.