Feladat: 905. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: könnyű
Megoldó(k):  Deák Jenő ,  Domokos László ,  Soltész Péter ,  Surányi László 
Füzet: 1964/december, 215 - 216. oldal  PDF  |  MathML 
Témakör(ök): Alakzatok szimmetriái, Tengelyes tükrözés, Pont körüli forgatás, Trapézok, Gyakorlat
Hivatkozás(ok):Feladatok: 1964/március: 905. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az AD és BC egyenesek metszéspontja M, és a kör középpontja O. A feltevések szerint M rajta van az AB átmérő fölötti Thalész-körön, továbbá O e kör AB-re merőleges átmérőjének egyik végpontja. Ezért az MO egyenes felezi az AMB szög mellékszögét, vagy magát az AMB szöget ‐ aszerint, hogy M az AB-nek O-t tartalmazó partján vagy az ellenkező parton adódott. Így az AD és BC egyenesek egymás tükörképei az MO tengelyre.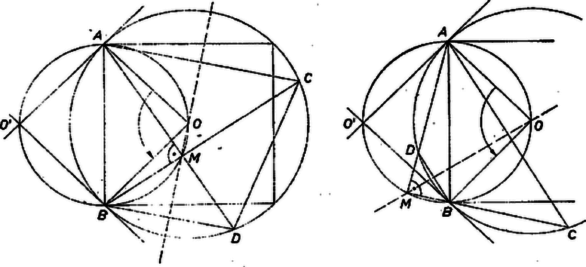
MO a körnek is szimmetriatengelye, ezért az AD, BC egyenespárral való A, D, B és C metszéspontjai két az MO-ra tükrös pontpárt alkotnak. A párokat összekötő egyenesek merőlegesek MO-ra, így egymással párhuzamosak, ezek a trapéz alapjai. Ezzel az állítást bebizonyítottuk. ‐ Az állítást így is kimondhatjuk: AC és BD párhuzamosak az MO' egyenessel, ahol O' az O tükörképe AB-re.
Ha M az AB egyenesnek O-t nem tartalmazó partján adódik, akkor a csúcspontokat A, B, C, D sorrendben összekötve hurkolt szimmetrikus trapézt kapunk.

 
 

Meggondolásunk nem alkalmazható arra az esetre, ha az MO egyenes határozatlan, vagyis ha M az O-ba esik. Az állítás ekkor is érvényes, mert így ABDC egy négyzet, és ez kétféleképpen is tekinthető szimmetrikus trapéznak.
Nem kapunk 4 különböző csúcsot, ha vagy az AD, vagy a BC egyenes egybeesik AB-vel, ekkor az állítás tárgytalan.
 
 Deák Jenő (Budapest, Kölcsey F. g. II. o. t.)
 

II. megoldás. Használjuk továbbra is az I. megoldás jelöléseit. Az M-nél derékszögű MAC és MBD derékszögű háromszögek további szögei 45∘-osak, mert ACM∢=ACB∢=45∘=MDB∢, mint az AB negyed köríven nyugvó kerületi szögek, ha M a BC szakaszon van, ‐ illetőleg az utolsó szög mint az ADBC húrnégyszög külső szöge, a szemben fekvő belső szöggel egyenlő, amennyiben M a CB szakasz meghosszabbításán van. Ezért MAC és MDB egyenlő szárú derékszögű háromszögek, M-ből húzott magasságuk vagy egymás meghosszabbítására esik, vagy közös szakaszuk van, ezért AC és BD átfogóik párhuzamosak. Így az ABCD négyszög húrtrapéz, ennélfogva egyszersmind szimmetrikus is.
 
Domokos László (Tatabánya, Árpád g. II. o.t.)
 Surányi László (Budapest, Fazekas M. g. I. o. t.)
 

III. megoldás. Feltevés szerint az AOB egyenlő szárú háromszög O-nál derékszögű. Így AD-t O körül 90∘-kal elforgatva úgy, hogy A a B pontba kerüljön, AD egy B-ből induló, AD-re merőleges húrba, tehát BC-be megy át. Az egyező irányú AD és BC ívek tehát egyenlők. Tükrözzük a kört a DB fölötti ívek felezőpontján átmenő átmérőre. Ekkor B átmegy D-be, a BC ív pedig a D-ből induló és BC-vel egyenlő, de vele ellentétes irányú ívbe, tehát DA-ba. Így C tükörképe A, tehát A, B, C, D egy szimmetrikus trapéz csúcsai.
 
 Soltész Péter (Budapest, I. István g. II. o. t.)