Kezdőlap


Feladat:	904. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Hámori Márta , Lamm Péter , Újvári István
Füzet:	1965/április, 150 - 153. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Középvonal, Kör (és részhalmaza), mint mértani hely, Parabola, mint mértani hely, Thalesz-kör, Látókörív, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/március: 904. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. I. Legyen a $B M$ húr felezőpontja $F$ , továbbá $A M$ és az $F$ -en át rá merőlegesen állított $m$ egyenes metszéspontja $T$ . Állítsunk merőlegest $A M$ -re $M$ -ben, jelöljük a körrel való, $M$ -től különböző metszéspontját $A'$ -vel, továbbá rajzoljuk meg az $A' B$ egyenest, és legyen ennek $m$ -mel közös pontja 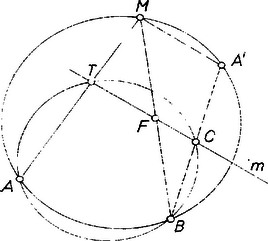$C$ .

1. ábra

F C

M A' B

háromszög középvonala, mert szerkesztésénél fogva párhuzamos

M A'

-vel,

F

pedig felezi az

M B

oldalt. Ennélfogva

C

A' B

oldal felezőpontja. ‐ Másrészt Thalész tételének megfordítása alapján

A'

a körnek

A

-val átellenes pontja, tehát

M

mozgása közben állandó, ezért állandó az

A' B

húr

C

felezőpontjának helyzete is. Eszerint

m

M

mozgása közben

C

körül forog. Ezt kellett bizonyítanunk.
Akkor is igaz az állítás, ha

M

egybeesik

A'

-vel vagy

B

-vel, mert

M = A'

esetén

F = C

, ha pedig

M = B

, akkor a

0

hosszúságú

B M

húr felezőpontjaként csak magát

B

-t tekinthetjük, és így

m

azonos

B A'

-vel, hiszen az

A B

-re

B

-ben állított merőleges ugyancsak

A'

-ben metszi a kört. Amikor

M

A

ponton halad át, az

M A

egyenes iránya határozatlan, ezért szigorúan véve

m

nem szerkeszthető meg. Tekintetbe véve azonban

M

mozgásának folytonosságát,

A M

irányaként csak az

A

-beli érintő iránya vehető, így fenti meggondolásunk érvényes marad.
Ha

A' = B

, vagyis

A

és

B

a kör átellenes pontjai voltak, akkor

M

minden helyzetében

M B ⊥ M A

, így

m = M B

, tehát

m

B

pont körül forog. (Ez adódik a fenti végeredményből is, ha az

A' B

húr

C

felezőpontjának ismét magát

B

-t tekintjük; minthogy azonban ilyenkor nem beszélhetünk az

M A' B

háromszögről és középvonaláról, külön meggondolást kellett végeznünk.)

II. Az eddigiek szerint a vizsgálandó

T

pontból az állandó

A C

szakasz derékszögben látható, ezért

T

mindig az

A C

átmérő fölé írt

t

Thalész-körön van. Megmutatjuk, hogy e kör minden pontja fellép

T

-ként, míg

M

befutja az eredeti kört. Legyen

t

egy tetszés szerinti pontja

T^{*}

, ekkor

M

-nek a

T^{*}

-ot előállító helyzetét az eredeti kör és az

{A T}^{*}

egyenes második metszéspontja jelöli ki,

T^{*} = A

esetén pedig a Thalész-kör

A

-beli érintője. Az

M

ponthoz a feladat szerint hozzárendelt

T

A M = {A T}^{*}

egyenes olyan pontja, melyből az

A C

szakasz derékszögben látszik, vagyis

{A T}^{*}

és

t

közös pontja. Ezeknek legfeljebb két közös pontja van:

A

és

T^{*}

. Csak akkor adódhat

T

-ként

A

, ha

C A

merőleges

A M

-re, azaz

{A T}^{*}

-ra, vagyis ha

{A T}^{*}

érinti a

t

kört, így

A

és

T^{*}

azonosak, tehát

T

T^{*}

-gal is egybeesik. Minden más helyzetben

A

és

T^{*}

különböző pontok, ezért

T

T^{*}

-gal azonos. Eszerint

T^{*}

valóban hozzátartozik a mértani helyhez, a keresett mértani hely az

A C

átmérő fölötti Thalész-kör.
A fenti módon

M

mindig létrejön, mert

{A T}^{*}

-nak és az eredeti körnek van közös pontja:

A;

amikor

T^{*}

az eredeti körhöz

A

-ban húzott érintőn van, akkor

M

azonos

A

-val.
Az

A' = B

helyzetben

t

azonos az eredeti körrel, minden más esetben a két kör

A

-ban és

B

-ben metszi egymást, ugyanis, mint láttuk,

A' B ⊥ A B

, tehát

B

t

-n is rajta van.

Ujvári István (Budapest, Fazekas M. gyak. g. I. o. t.)
Lamm Péter (Budapest, Rákóczi F. g. II. o. t.)

2. ábra

II. megoldás a feladat első részére. Külön vizsgáljuk azt az esetet, ha

M

A

vagy

B

, vagy az átellenes

A'

vagy

B'

pontban van (2. ábra), majd külön a kör ezektől különböző

M

pontjait. Ha

B'

-vel esik egybe

M

, akkor

M B

felezőpontja a kör

O

középpontja, másrészt

M A

merőleges

A B

-re, tehát a vizsgálandó merőleges az

O

-n átmenő,

A B

-vel párhuzamos

c

egyenes; az állításban szereplő állandó pont csak ezen lehet. ‐ Legyen másodszor

M

A'

pontban. Az

A B A' B'

négyszög téglalap, és ennek egyik szimmetriatengelye

c

, másrészt az

M B = A' B

szakasz

C

felezőpontja rajta van

c

-n. A keresett állandó pont csak

C

lehet, mert a

C

-ből

M A = A' A

-ra állított merőleges különbözik

c

-től, hiszen

A' A

hegyes szöget zár be a

c

-vel párhuzamos

A B

-vel. ‐

C

-n megy át a merőleges az

M = B

esetben is, mert ekkor

B M

felezőpontja maga

B

, így

M A

azonos

B A

-val, a merőleges a

B A'

egyenes.
Amikor

M

A

-n halad át, az

M A

egyenes határozatlan. A vizsgálandó merőleges irányát azonban megadhattuk volna így is: párhuzamos az

A M

szakasz felezőpontját az

O

középponttal összekötő egyenessel. Így az

M = A

helyzetben a merőleges átmegy

A B

-nek

D

felezőpontján és párhuzamos

A O

-val, tehát az

A B A'

háromszög

A A'

-vel párhuzamos középvonala, felezi

B A'

-t

C

-ben.
Legyen most már

M

a körnek

A

-tól,

B

-től,

A'

-től és

B'

-től különböző pontja. Megmutatjuk, hogy az

M B

húr

F

felezőpontján át

M A

-ra állított merőleges átmegy

C

-n. Ehhez elég azt megmutatni, hogy

C F ⊥ A M

, mert

F

-ből csak egy merőleges állítható

A M

-re, annak tehát egybe kell esnie

C F

-fel, ha állításunk igaz. A bizonyítandó állítás következik abból, ha megmutatjuk, hogy

C O E F

paralelogramma, mert ekkor

C F ∥ E O

, az utóbbi viszont az

A M

húr felező merőlegese. Mivel

E F

A B M

háromszög középvonala,

O C

pedig az

A B A'

háromszögé, így mindkettő párhuzamos

A B

-vel és feleakkora, tehát egymással is párhuzamosak és egyenlők;

C O E F

tehát valóban paralelogramma. Ezzel az állítást bebizonyítottuk.

Hámori Márta (Győr, Kazinczy F. g. II. o. t.)

Megjegyzés. Közel vezet a feladat állításának bebizonyításához a következő meggondolás is. Legyen a mozgó pont két tetszés szerinti helyzete

M_{1}

és

M_{2}

, legyen

i = 1, 2

esetén a

B M_{i}

húr felezőpontja

F_{i}

, ennek merőleges vetülete az

A M_{i}

egyenesen

T_{i}

, az

F_{i} T_{i}

az egyenes

m_{i}

, végül

m_{1}

és

m_{2}

metszéspontja

C

(ez létezik, mert

A M_{1}

nem párhuzamos

A M_{2}

-vel, 3. ábra). ‐ Az

F_{1} C F_{2}

szög vagy egyenlő az

M_{1} A M_{2}

szöggel, vagy annak kiegészítő szöge, mert száraik páronként merőlegesek egymásra. Az

M_{1} B M_{2}

szög vagy egyenlő az

M_{1} A M_{2}

szöggel, vagy annak kiegészítő szöge, mert az adott körben vagy ugyanazon

M_{1} M_{2}

íven nyugvó kerületi szögek ‐ ha ti. az

M_{1} M_{2}

egyenes nem választja szét

A

-t és

B

-t ‐, szétválasztás esetén pedig

A

és

B

A M_{1} B M_{2}

húrnégyszög szemben fekvő csúcsai. Így az

F_{1} C F_{2} ∢

vagy egyenlő az

F_{1} B F_{2} ∢

-gel (mert az utóbbi azonos az

M_{1} B M_{2} ∢

-gel), vagy annak kiegészítő szöge, vagyis az

F_{1} F_{2}

szakasz

C

-ből vett látószöge egyenlő a

B

-ből vett látószögével, vagy kiegészítő szögek.

3. ábra

Mármost

F_{1}

és

F_{2}

rajta van az

O B

átmérőjű

k'

Thalész-körön, ezért

C

vagy a

k'

-n van, vagy annak az

F_{1} F_{2}

egyenesre való tükörképén. Feltéve, hogy az első eset áll fenn, rögzítsük

M_{1}

-et, és fussa be

M_{2}

az adott kört. A fentiek szerint

m_{2}

ugyanott metszi

k'

-t, mint

m_{1}

, vagyis

C

-ben, eszerint amíg

M_{1}

nem változik,

C

állandó pont. Másrészt

F_{2}

körülfut

k'

-n, tehát

m_{2}

teljesen körülfordul

C

körül. Eszerint ‐ ha egyáltalán van állandó pont ‐ az csak

C

lehet.
Hátra van még annak bizonyítása, hogy

C

helyzete független

M_{1}

megválasztásától, továbbá hogy

C

nem lehet

k'

-nek

F_{1} F_{2}

-re való tükörképén.