Kezdőlap


Feladat:	898. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Augusztinovicz Fülöp , Babai László , Hoffer Anna , Kiss Árpád , Reményi Katalin
Füzet:	1964/november, 150 - 153. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középpontos tükrözés, Sokszög lefedések, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/február: 898. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Bontsuk fel a vizsgálandó $E F G H$ négyszöget az $E G$ átlóval az $E F G$ és $G H E$ háromszögekre (1. ábra). Az előbbinek a területe nyilvánvalóan egyenlő az $A E G$ háromszög területével, az utóbbié a $C G E$ háromszögével, így az $E F G H$ négyszög területe egyenlő az $A E C G$ négyszög területével.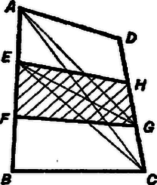

1. ábra

Bontsuk fel ezt az

A C

átlóval az

A E C

és

C G A

háromszögekre. Az előbbinek a területe harmadrésze az

A B C

háromszög területének, az utóbbié pedig a

C D A

háromszögének, így az

A E C G

négyszög területe ‐ tehát az

E F G H

négyszögé is ‐ egyenlő az

A B C

és

C D A

háromszögekkel kitöltött

A B C D

négyszög területének harmadrészével. Ezzel az állítást bebizonyítottuk.

Reményi Katalin (Budapest, XI. ker. Szamuely T. ált. isk. 8. o. t.)

Megjegyzés. Az utolsó lépésig csak azt használtuk fel, hogy az

A E

és

E F

, valamint

C G

és

G H

szakasz-párok egyenlők, nem volt szó az

F B

és

H D

szakaszról. Ha tehát

A E

és

E F

pl. negyedrésze volna

A B

-nek, és

C G

és

G H

ugyancsak negyedrésze

C D

-nek, akkor az

E F G H

négyszög területe negyedrésze lenne az

A B C D

négyszög területének.

II. megoldás. Tükrözzük ábránkat az

A B

oldal és az

E F

szakasz közös

K

felezőpontjára, és legyen

C

G

H

D

tükörképe rendre

C^{*}

G^{*}

H^{*}

D^{*}

(2. ábra). Így elég azt megmutatnunk, hogy az

E G^{*} H^{*} F G H = S_{1}

és

A C^{*} D^{*} B C D

centrálisan szimmetrikus hatszögek területeinek aránya

1 : 3

, vagy másképpen ‐ mivel a

B C G F H^{*} D^{*}

hatszög az

A C^{*} G^{*} E H D = S_{2}

hatszög tükörképe, és így területük egyenlő ‐, hogy az

S_{1}

és

S_{2}

hatszögek területe egyenlő.

2. ábra

Megrajzolva a

G G^{*}

H H^{*}

A H

és

A G^{*}

átlókat, a

K E H

és

K F H^{*}

háromszögek egybevágók, területük összege egyenlő az

A E H

háromszög területével, mert ennek

H

-ból induló magassága közös a

K E H

háromszöggel,

A E

alapja pedig kétszerese

E K

-nak. Ugyanígy a

K F G

és

K E G^{*}

háromszögek területének összege egyenlő az

A E G^{*}

háromszög területével. Végül a

K G H

és

K G^{*} H^{*}

háromszögek területének összege és az

A H D

és

A C^{*} G^{*}

háromszögek területének összege is egyenlő, mert a párhuzamos

C D

és

C^{*} D^{*}

egyenesekbe eső oldalaik egyenlők, és az erre merőleges magasságaik összege egyenlő a mondott két egyenes távolságával. Így az

S_{1}

-ben és

S_{2}

-ben keletkezett valamennyi rész-idom területeinek összege egyenlő. Ezt akartuk bizonyítani.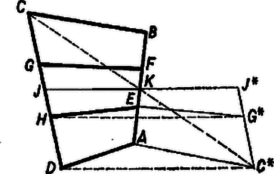

Hoffer Anna (Budapest, Hámán K. g. III. o. t.)

3. ábra

III. megoldás. Legyen ismét

A B

és

E F

közös felezőpontja

K

, továbbá

C D

és

G H

közös felezőpontja

J

(3. ábra). Tükrözzük

K

-ra a

K B C J

négyszöget, jelöljük

C

G

J

tükörképét

C^{*}

J^{*}

G^{*}

-gal;

B

és

F

tükörképe

A

, ill.

E

. A feladat állítása az

A C^{*} J^{*} J D = T

ötszögre fogalmazva annak bizonyítását kívánja, hogy területe háromszor akkora, mint az

E G^{*} J^{*} J H = T_{1}

ötszögé. Meghúzva a

C^{*} D

és

G^{*} H

átlókat, a

T

ötszög a

J D C^{*} J^{*}

paralelogrammából úgy áll elő, hogy ahhoz a

D A C^{*}

háromszöget vagy hozzáillesztjük, vagy kivágjuk belőle (az ábrán az utóbbit látjuk), és ugyanígy áll elő a

T_{1}

ötszög a

J H G^{*} J^{*}

paralelogrammából és a

H E G^{*}

háromszögből; lehetséges az is, hogy

C^{*} D

átmegy

A

-n, ekkor

G^{*} H

is átmegy

E

-n, és így mindegyik ötszög területe egyenlő a megfelelő paralelogrammáéval.
Az ötszögek és részeik összehasonlításában közös alapnak a

C^{*} D = J^{*} J = G^{*} H

szakaszt véve elég azt belátnunk, hogy

D

-nek

J^{*} J

fölötti magassága

3

-szor akkora, mint

H

-é, továbbá hogy

A

-nak

C^{*} D

fölötti magassága

3

-szor akkora, mint

E

-nek

G^{*} H

fölötti magassága. Az első következik abból, hogy nyilvánvalóan

J D = 3 J H

, a második pedig a

K A = 3 K E

egyenlőségből, meggondolva még, hogy

A

és

E

kívánt magasságát a paralelogrammák magasságaiból, valamint

J^{*} J

fölötti magasságaikból kapjuk, mindig a nagyobból vonva ki a kisebbet.

Babai László (Budapest, VIII. ker., Somogyi B. u. ált. isk. 8. o. t.)

4. ábra

IV. megoldás. Húzzuk meg az

A H

E G

F C

szakaszokat és bocsássunk merőlegest

A B

-re a

H

G

C

pontokból, valamint

C D

-re

A

-ból,

E

-ből és

F

-ből, legyen ezek hossza rendre

m_{1}

m_{2}

m_{3}

, illetőleg

m_{4}

m_{5}

m_{6}

(4. ábra). Az így

6

háromszögre felosztott

A B C D

négyszög területe

\begin{matrix} \frac{C D}{6} (m_{4} + m_{5} + m_{6}) + \frac{A B}{6} (m_{1} + m_{2} + m_{3}), \end{matrix}

E F G H

négyszög területe pedig

\begin{matrix} \frac{C D}{6} \cdot m_{5} + \frac{A B}{6} \cdot m_{2} . \end{matrix}

Elég megmutatnunk, hogy az első terület zárójeles kifejezései rendre

3

-szor akkorák, mint a másodikban az

m_{5}

, ill.

m_{2}

tényező.
Ez fennáll, mert az

m_{1}

és

m_{3}

párhuzamos oldalakkal meghatározott trapézben

m_{2}

középvonal, így

m_{1} + m_{3} = 2 m_{2}

, mindkét oldalhoz

m_{2}

-t adva

m_{1} + m_{2} + m_{3} = 3 m_{3}

, és ugyanígy

m_{4} + m_{5} + m_{6} = 3 m_{5}

. Ezzel az állítást bebizonyítottuk.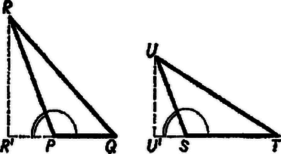

Augusztinovicz Fülöp (Sopron, Széchenyi I. g. I. o. t.)

5. ábra

V. megoldás. Megmutatjuk, hogy ha két háromszögnek egy-egy szöge egyenlő, akkor területeik aránya megegyezik az egyenlő szögeket bezáró oldalak szorzatainak arányával. Legyen egyenlő a

P Q R

háromszög

Q P R

szöge az

S T U

háromszög

T S U

szögével, továbbá az

R

, ill.

U

csúcs vetülete a szemben levő oldalon

R'

, ill.

U'

(5. ábra). Ekkor, felhasználva a

P R R'

és

S U U'

derékszögű háromszögek hasonlóságát:

\begin{matrix} \frac{t_{P Q R}}{t_{S T U}} = \frac{P Q \cdot R R'}{S T \cdot U U'} = \frac{P Q}{S T} \cdot \frac{R R'}{U U'} = \frac{P Q}{S T} \cdot \frac{P R}{S U} = \frac{P Q \cdot P R}{S T \cdot S U} . \end{matrix}

Ezt így is írhatjuk:

\begin{matrix} t_{P Q R} = k \cdot P Q \cdot P R és t_{S T U} = k \cdot S T \cdot S U, \end{matrix}

ahol

k

alkalmas szám (csak a

P

-nél, ill.

S

-nél levő szög nagyságától függ).
Ha az

A B C D

négyszögben

C D

párhuzamos

A B

-vel, akkor az állítás helyessége nyilvánvaló, mert a két szóban forgó négyszög egyenlő magasságú trapéz és bennük a megfelelő alap-párok aránya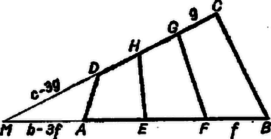

1 : 3

6. ábra

Az ellenkező esetben az

A B

és

C D

oldalak

M

metszéspontja a konvexség miatt ezen oldalak meghosszabbításán van; válasszuk a betűzést úgy, hogy

M A < M B

, és így

M D < M C

(6. ábra), legyen továbbá

M B = b

M C = c

F B = f

G C = g

, ezekkel

\begin{matrix} \begin{matrix} M F = b - f, & M E = b - 2 f, & M A = b - 3 f, \\ M G = c - g, & M H = c - 2 g, & M D = c - 3 g \end{matrix} \end{matrix}

(mind pozitívok). Az

A B C D

négyszög területe egyenlő az

M B C

és

M A D

háromszögek területének különbségével,

E F G H

-é pedig az

M F G

és

M E H

háromszögekével. E négy háromszög

M

-nél levő szöge közös, így fenti segédtételünk szerint

\begin{matrix} t_{A B C D} & = t_{M B C} - t_{M A D} = k (M B \cdot M C - M A \cdot M D) = \\ = k [b c - (b - 3 f) (c - 3 g)] = 3 k (b g + c f - 3 f g), \\ t_{E F G H} & = t_{M F G} - t_{M E H} = k (M F \cdot M G - M E \cdot M H) = \\ = k [(b - f) (c - g) - (b - 2 f) (c - 2 g)] = k (b g + c f - 3 f g), \end{matrix}

amiből az állítás helyessége nyilvánvaló.

Kiss Árpád (Budapest, Bláthy O. erősár. ip. t. II. o. t.)

Megjegyzés. A felhasznált segédtétel akkor is helyes, ha a két háromszög egy-egy szöge egymásnak kiegészítő szöge.