Kezdőlap


Feladat:	897. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Berkes István , Király László
Füzet:	1964/november, 148 - 150. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Deltoidok, Érintőnégyszögek, Párhuzamos szelők tétele és megfordítása, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/február: 897. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a feltételeknek megfelelő $A B C D$ deltoid szimmetria-tengelye az $A C$ egyenes, így 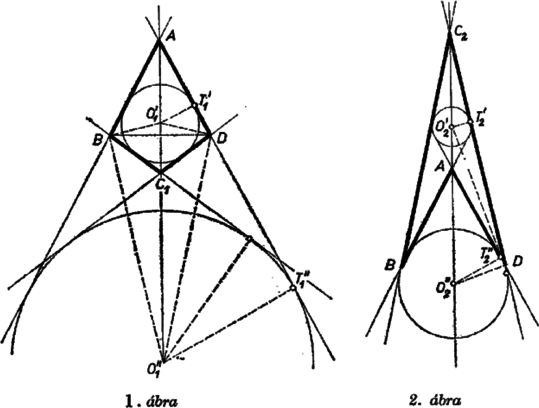$A C = 21$ , $B D = 16$ , továbbá $A B = 17$ egység.

A C

és

B D

metszéspontját

M

-mel jelölve az

A B M

derékszögű háromszögből Pythagorász tétele alapján

A M = 15

. Ha

C

A M

szakasz

M

-en túli meghosszabbításán van, akkor

A B C_{1} D

konvex deltoid (1. ábra), ha pedig az

A

-n túli meghosszabbításon, akkor

A B C_{2} D

konkáv deltoid (2. ábra). Az előbbiben

M C_{1} = A C_{1} - A M = 6

, és így

C_{1} B = 10

, a másodikban

M C_{2} = A C_{2} + A M = 36

, és így

C_{2} B = \sqrt[]{1360} = 4 \sqrt[]{85}

Mindkét deltoid esetében

2

olyan kör szerkeszthető, amely mindegyik oldal egyenesét érinti. Ugyanis a kör középpontja egyrészt az

A C

tengelyen van, ami az

A

-nál és

C

-nél levő szögek egybeeső felezője, másrészt például az

A B

B C

egyenespár közti szögek valamelyikének felezőjén; márpedig

2

szögfelező van, és mindegyik metszi a tengelyt, mert az

A B C

háromszög sem a konvex, sem a konkáv deltoid esetében nem egyenlő szárú. A metszéspontok körül az

A B

és

B C

egyeneseket érintő kört rajzolva, ez a szimmetria miatt az ezekre tükrös

A D

D C

egyeneseket is érinti.

Meggondolásunkat folytatva kiszámítjuk a körök középpontjának

A

-tól mért távolságát, majd ebből a sugarát. Messe a tengelyt az

A B C_{i}

háromszög

B

-nél levő belső szögének felezője

O'_{i}

-ben, a külső szögé

O''_{i}

-ben

(i = 1, 2)

. Ekkor a szögfelező osztásarányára ismert tétel szerint mindegyik középpont esetében

\begin{matrix} A O : C_{i} O = A B : C_{i} B, \end{matrix}

és mivel a belső szögfelezők

A C_{i}

-vel való metszéspontjára

A O'_{i} + O'_{i} C_{i} = A C_{i}

, a külsőkre pedig

A O_{1}'' - C_{1} O_{1}'' = A C_{1}

, ill.

C_{2} O''_{2} - A O''_{2} = C_{2} A

(ugyanis

A B > B C_{1}

és

C_{2} B > A B

), azért

\begin{matrix} A O_{i} = A C_{i} \frac{A B}{A B + C_{i} B}; A O'_{1} = \frac{119}{6}, A O'_{2} = \frac{357}{17 + 4 \sqrt[]{85}} = \frac{1}{3} (4 \sqrt[]{85} - 17); \\ A O''_{1} = A C_{1} \frac{A B}{A B - C_{1} B} = 51, \\ A O''_{2} = A C_{2} \frac{A B}{C_{2} B - A B} = \frac{357}{4 \sqrt[]{85} - 17} = \frac{1}{3} (4 \sqrt[]{85} + 17) . \end{matrix}

Legyen végül a kör érintési pontja az

A B

egyenesen

T

(azaz

T'_{1}

T''_{1}

T'_{2}

T''_{2}

), akkor a közös hegyesszöggel bíró

A O T

és

A B M

derékszögű háromszögek hasonlóságából az érintő kör sugara bármelyik kör esetére

\begin{matrix} O T = r = M B \cdot \frac{A O}{A B} = \frac{8}{17} A O, \end{matrix}

és a

4

körre rendre

\begin{matrix} r'_{1} = \frac{56}{9}, r''_{1} = 24, r'_{2} = \frac{8}{51} (4 \sqrt[]{85} - 17) \approx 3, 12, \\ r''_{2} = \frac{8}{51} (4 \sqrt[]{85} + 17) \approx 8, 45. \end{matrix}

Király László (Budapest, Eötvös J. g. II. o. t.)

II. megoldás. Az érintő körök sugarát megkaphatjuk a deltoid

t

területének kétféle kifejezéséből. Egyrészt

t = A C \cdot B D / 2

, másrészt a belső érintő körök esetében,

t

ama négy háromszög területének összege, amelyekre a deltoid oszlik, ha csúcsait összekötjük a beírt kör középpontjával. E háromszögek alapjainak az egymás utáni oldalakat véve, magasságuk a beírt kör

r'_{i}

sugara, tehát

\begin{matrix} 2 t = r'_{i} (2 A B + 2 C_{i} B) = A C \cdot B D, \\ r'_{1} = \frac{56}{9}, r'_{2} = \frac{8}{51} (4 \sqrt[]{85} - 17) . \end{matrix}

A külső érintő körök esetében a csúcsok és

O''_{i}

összekötésével előálló háromszögek területéből úgy kapjuk a deltoid területét, ha alkalmasan választott kettőjük területének összegéből kivonjuk a másik két háromszög területének összegét. A területeket ugyanúgy jelölve, mint magukat az idomokat:

\begin{matrix} t & = A B O''_{1} D - C_{1} B O''_{1} D = (A B O''_{1} + A D O''_{1}) - (C_{1} B O''_{1} + C_{1} D O''_{1}) = \\ = r''_{1} (A B - C_{1} B) = \frac{A C_{1} \cdot B D}{2}, \\ t & = C_{2} B O''_{2} D - A B O''_{2} D = (C_{2} B O'_{2} + C_{2} D O''_{2}) - (A B O''_{2} + A D O''_{2}) = \\ = r''_{2} (C_{2} B - A B) = \frac{A C_{2} \cdot B D}{2}; \\ r''_{1} & = \frac{A C_{1} \cdot B D}{2 (A B - C_{1} B)} = 24, r''_{2} = \frac{A C_{2} \cdot B D}{2 (C_{2} B - A B)} = \frac{8}{51} (4 \sqrt[]{85} + 17) . \end{matrix}

Berkes István (Budapest, Fazekas M. g. II. o. t.)

Megjegyzés. Több versenyző a koordináta-geometria módszereivel is megoldotta a feladatot.