Kezdőlap


Feladat:	890. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Arányi Péter , Bárány I. , Baranyai Zs. , Bóta K. , Deák J. , Domokos Zsuzsanna , Fodor Magdolna , Halász Szilvia , Horváth J. (Bp., Fazekas g.) , Huhn A. , Karsa Kornélia , Király L. , Kiss A. , Kloknicer J. , Kotsis Erzsébet Kinga , Kövér Á. , Laczkovich M. , Major P. (Bp. Fazekas g.) , Malina J. , Mátrai M. , Nagy Klára , Siket Aranka , Szeidl L. , Szentiványi B. , Tolnay-Knefély T. , Treer Mária , Trieb K. , Vesztergombi Katalin
Füzet:	1965/február, 60 - 62. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenletrendszerek, Inverzió, Síkgeometriai számítások trigonometria nélkül körökben, Körérintési szerkesztések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1964/január: 890. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

a) Az alábbi 3 észrevételre támaszkodva alkalmas sorrendben kifejezzük a körök sugarait és középpontjuk távolságát az ábra alkalmas pontjaitól, az ábra befoglaló körének sugarával, ezek alapján az ábra megszerkeszthető lesz. A 2. ábra jelöléseit használjuk.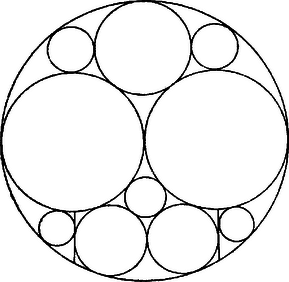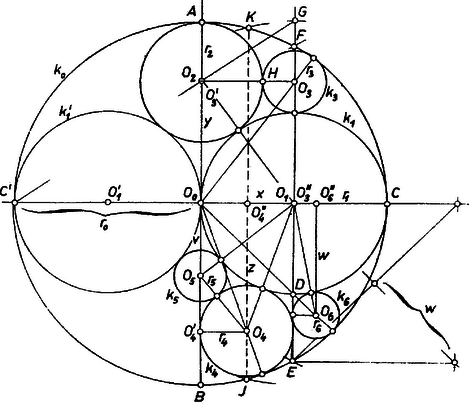

1. ábra

2. ábra

I. Az 1. ábrán 11 kör és 2 egyenesszakasz látható; az ábra szimmetrikus a 2. ábra

A B

egyenesére.
II. A

k_{1}

és

k'_{1}

körök

A B

-nek

O_{0}

felezőpontjában érintik egymást.
III. A

D E

egyenesszakasz párhuzamos

A B

-vel.
Az I. észrevétel szerint

A B

k_{0}

kör átmérője,

O_{0}

a középpontja. A 4 tükrös körpárból, valamint az egyenesszakasz‐párból elég 1‐1 kört, ill. szakaszt megszerkesztenünk, továbbá felhasználhatjuk, hogy

O_{2}

és

O_{5}

A B

átmérőn van. II. szerint az

O_{0} O_{1}

egyenes ugyancsak átmérőt metsz ki

k_{0}

-ból, ezen van

k_{0}

és

k_{1}

érintkezési pontja,

C

, és így

r_{1} = r_{0} / 2

.
Az

O_{1} O_{2} O_{0}

derékszögű háromszögben

k_{1}

és

k_{2}

érintkezése miatt

O_{1} O_{2} = r_{1} + r_{2}

O_{0} O_{2} = r_{0} - r_{2}

, mert

k_{2}

A

-ban érinti

k_{0}

-t, és így Pythagoras tétele alapján

\begin{matrix} O_{1} O_{2}^{2} - O_{0} O_{2}^{2} = {(r_{1} + r_{2})}^{2} - {(r_{0} - r_{2})}^{2} = (2 r_{2} + r_{1} - r_{0}) (r_{0} + r_{1}) = \\ = O_{0} O_{1}^{2} = r_{1}^{2}, \\ r_{2} = \frac{1}{2} (\frac{r_{1}^{2}}{r_{0} + r_{1}} + r_{0} - r_{1}) = \frac{r_{0}}{3} . \end{matrix}

Legyen

O_{3}

vetülete

A B

-n

O'_{3}

O_{0} C

-n

O''_{3}

, és

O_{0} O'_{3} = O''_{3} O_{3} = y

O_{0} O''_{3} = O'_{3} O_{3} = x

k_{3}

érintkezései miatt

O_{0} O_{3} = r_{0} - r_{3}

O_{1} O_{3} = r_{1} + r_{3}

O_{2} O_{3} = r_{2} + r_{3}

, és így az

O_{0} O_{3} O'_{3}

O_{1} O_{3} O''_{3}

O_{2} O_{3} O'_{3}

derékszögű háromszögekből

\begin{matrix} x^{2} + y^{2} = {(r_{0} - r_{3})}^{2}, & (1) \\ {(x - r_{1})}^{2} + y^{2} = {(r_{1} + r_{3})}^{2}, & (2) \\ x^{2} + {(y - 2 r_{2})}^{2} = {(r_{2} + r_{3})}^{2}, & (3) \end{matrix}

ugyanis

O_{1} O''_{3} = | O_{0} O''_{3} - O_{0} O_{1} | = | x - r_{1} |

, másrészt a fentiek szerint

O_{0} O_{2} = r_{0} - r_{2} = 2 r_{2}

, és így hasonlóan

O_{2} O'_{3} = | y - 2 r_{2} |

. Kivonva (1)-ből (2)-t, majd (3)-at, és felhasználva a kínálkozó szorzattá alakítási lehetőségeket, valamint eddigi eredményeinket:

\begin{matrix} r_{1} (2 x - r_{1}) & = (r_{0} + r_{1}) (r_{0} - r_{1} - 2 r_{3}), x = r_{0} - 3 r_{3}, \\ 4 r_{2} (y - r_{2}) & = (r_{0} + r_{2}) (r_{0} - r_{2} - 2 r_{3}), y = r_{0} - 2 r_{3}, \end{matrix}

és ezeket (1)-be helyettesítve

\begin{matrix} 12 r_{3}^{2} - 8 r_{0} r_{3} + r_{0}^{2} = 0, \end{matrix}

amiből

r'_{3} = r_{0} / 6

r''_{3} = r_{0} / 2

. A második gyökkel

x = - r_{1}

y = 0

, vagyis

O''_{3} = O'_{1}

és

k'_{1}

-t kapjuk, amely valóban ugyancsak belülről érinti

k_{0}

-t, és kívülről érinti

k_{1}

-et,

k_{2}

-t, most azonban nem ezt keressük. Így

r_{3} = r_{0} / 6

x = r_{0} / 2 = r_{1}

y = 2 r_{0} / 3

, vagyis

O''_{3} = O_{1}

O_{3} = O_{2}

k_{4}

érinti

k_{0}

-t,

k_{1}

-et és

A B

-t, így

O_{4} O''_{1}

-t

z

-vel jelölve az

O_{0} O_{4} O''_{4}

és

O_{1} O_{4} O''_{4}

derékszögű háromszögekből,

O_{4} O''_{4} = O'_{4} O_{4} = r_{4}

figyelembevételével

\begin{matrix} r_{4}^{2} + z^{2} = {(r_{0} - r_{4})}^{2}, {(r_{1} - r_{4})}^{2} + z^{2} = {(r_{1} + r_{4})}^{2} . \end{matrix}

z

kiküszöbölésével

r_{4} = r_{0} / 4

, ebből pedig

z = r_{0} / \sqrt[]{2}

k_{5}

érinti

k_{1}

-et és

k_{4}

-et, és

O_{5}

A B

-n van;

O_{0} O_{5} = v

jelöléssel

O_{5} O'_{4} = z - v

, és az

O_{0} O_{1} O_{5}

O_{4} O'_{4} O_{5}

derékszögű háromszögekből

\begin{matrix} v^{2} = {(r_{1} + r_{5})}^{2} - r_{1}^{2}, {(z - v)}^{2} = {(r_{4} + r_{5})}^{2} - r_{4}^{2} . \end{matrix}

Az utóbbit az előbbiből kivonva

\begin{matrix} 2 z v = z^{2} + 2 (r_{1} - r_{4}) r_{5}, v = (r_{0} + r_{5}) / 2 \sqrt[]{2}, \end{matrix}

és ezt az előbbibe helyettesítve

\begin{matrix} 7 r_{5}^{2} + 6 r_{0} r_{5} - r_{0}^{2} = 0, amiből r'_{5} = - r_{0} / 7, r''_{5} = - r_{0} . \end{matrix}

A második gyökkel

v = 0

, vagyis ekkor a keresett kör középpontja azonos

O_{0}

-lal, és a sugár abszolút értéke

r_{0}

. Eszerint

k''_{5}

-ként maga

k_{0}

jön szóba. Valóban

k_{0}

megfelel a fenti követelményeknek, de

k_{1}

-gyel és

k_{4}

-gyel belső érintkezésben van a várt külső érintkezéssel szemben; ezt fejezi ki

r''_{5}

negatív volta. A számunkra megfelelő gyök

r_{5} = r_{0} / 7

, evvel

v = 4 r_{0} / 7 \sqrt[]{2} = 4 z / 7

.
A III. észrevétel szerint a

D E

szakasz távolsága

A B

-től

2 r_{4} = r_{0} / 2 = r_{1}

, vagyis

D E

meghosszabbítása átmegy

O_{1}

-en.
Végül

k_{6}

érinti

k_{0}

-t belülről,

k_{1}

-et kívülről és a

D E

egyenest. Az

O_{0} O_{6} O''_{6}

és

O_{1} O_{6} O''_{6}

derékszögű háromszögekből

O_{6} O''_{6} = w

jelöléssel, felhasználva az előbbi megállapítást is,

\begin{matrix} w^{2} = {(r_{0} - r_{6})}^{2} - {(r_{1} + r_{6})}^{2} = {(r_{1} + r_{6})}^{2} - r_{6}^{2}, \end{matrix}

amiből

r_{6} = r_{0} / 8

, és

w = \sqrt[]{3} r_{0} / 2 \sqrt[]{2}

b) Mindezek alapján az 1. ábra pl. a következő lépésekben szerkeszthető:
‐1. Az

r_{0}

sugarú

k_{0}

körben megrajzoljuk az egymásra merőleges

A B

és

C C'

átmérőket.
‐ 2.

C

körül

r_{0}

sugárral

k'_{0}

kört írunk, ez

k_{0}

-t az

E

F

pontokban (

F

A C

negyedköríven), az

E F

egyenes

C C'

-t

O_{1}

-ben metszi. Megszerkesztjük e vonalak

A B

-re való tükörképét (ezt a továbbiak során is mindig megtesszük, bár külön nem említjük). Az

O_{1}

körül

O_{1} O_{0}

sugárral írt kör

k_{1}

, ennek

E F

-fel való metszéspontja

D

, a

C C'

-nek

B

-t tartalmazó partján.
‐ 3. Az

O_{1} F

félegyenesre felmérjük az

O_{1} G = r_{0}

szakaszt, a

C' G

egyenessel

A B

-ből kimetsszük

O_{2}

-t, az

O_{2}

körül

O_{2} A

sugárral írt kör

k_{2}

.
‐ 4. Az

O_{2}

-n átmenő,

C C'

-vel párhuzamos egyenes

E F

-et

O_{3}

-ban,

k_{2}

-t

H

-ban metszi (

A B

-nek

C

-t tartalmazó partján), az

O_{3}

körül

O_{3} H

sugárral írt kör

k_{3}

.
‐ 5. Az

O_{1}

körül

r_{0}

sugárral írt kör

k_{0}

-t

J

-ben és

K

-ban metszi, a

J K

egyenes

C C'

-ből kimetszi

O''_{4}

-t; felmérjük

O_{0} D

-t az

O_{0} B

és

O''_{4} J

félegyenesre, a végpont

O'_{4}

, ill.

O_{4}

, az

O_{4}

körül

O_{4} O'_{4}

sugárral írt kör

k_{4}

.
‐ 6. Az

O_{0} O'_{4}

szakaszt 7 egyenlő részre osztjuk, az

O_{0}

-tól számított negyedik osztópont

O_{5}

; az

O_{4} O_{5}

félegyenesnek

k_{4}

-gyel való metszéspontja¹

N

; az

O_{5}

körül

O_{5} N

sugárral írt kör

k_{5}

. ‐ 7. Az

O_{1} C

szakaszt 4 egyenlő részre osztjuk, az

O_{1}

-től számított első osztópont

O''_{6}

;

O_{1} E

oldalú négyzetet szerkesztünk, ennek középpontja

P

; az

O_{1} P

szakaszt felmérjük az

O''_{6}

-ben

C C'

-re állított merőlegesre (a

B

-t tartalmazó parton), a végpont

O_{6}

; végül az

O_{6}

körül

O_{1} O''_{6}

sugárral írt kör

k_{6}

.
A közölt eljárás lépéseinek helyessége az a) részben végzett számítások alapján bizonyítható. Ennek végrehajtását ‐ hely hiányában ‐ az olvasóra hagyjuk.

Treer Mária (Budapest, Kaffka M. g. III. o. t.)
Kotsis Erzsébet Kinga (Budapest, Fehérvári úti 12 évf. isk. II. g. o. t.)

Megjegyzés. Inverzió módszerével ² a szerkesztés számítások nélkül is elvégezhető, másrészt a számítások nagy része is egyszerűbben végezhető.
Arányi Péter (Budapest, Apáczai Csere J. gyak. g. II. o. t.)

¹Az ábrán

N

és az alábbi

P

pótlandó.

²Lásd pl. Faragó László‐Forgó Péterné: Geometriai szerkesztések 2. kiadás (Középiskolai Szakköri Füzetek, Tankönyvkiadó, Budapest, 1954) 19‐27. o.