Feladat: 888. matematika gyakorlat Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bárány I. ,  Berényi J. ,  Czina F. ,  Domokos Zsuzsanna ,  Havas J. ,  Király L. ,  Kiss A. ,  Kóbor Gy. ,  Major Péter ,  Sarkadi Nagy I. ,  Siket Aranka ,  Staub Klára ,  Surányi L. 
Füzet: 1965/február, 57 - 59. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Pont körüli forgatás, Vetítések, Mozgási geometria, Gyakorlat
Hivatkozás(ok):Feladatok: 1964/január: 888. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Vizsgáljuk először a kérdéses β szög változását abban az esetben, ha a=MON∢ hegyes szög.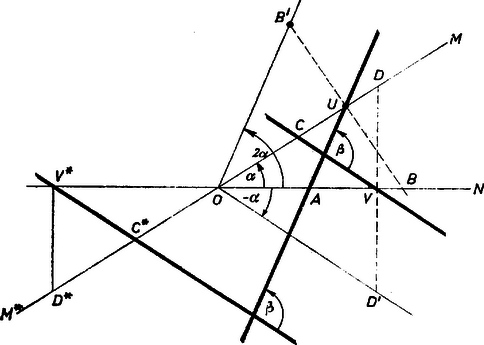

 
 
1. ábra
 

A feltételek azt jelentik, hogy A az OB szakasz felezőpontja, C pedig OD-é. Tükrözzük B-t az OM, D-t pedig az ON egyenesre, legyen a kép B', ill. D' (1. ábra). Így U felezi a BB' szakaszt, ezért AU az OBB' háromszög OB'-vel párhuzamos középvonala. Hasonlóan CV párhuzamos OD'-vel, ennélfogva az AU, CV egyenespár közti szögek egyállásúak az OB', OD' egyenespár közti szögekkel és így egyenlők velük.
Ámde OB' az ON egyenes tükörképe OM-re, és így ON-ből OB'-be 2α nagyságú forgás visz át ‐ ugyanabban az irányban, amelyben OM fordult el ON-ből. OD' pedig OM tükörképe ON-re, és így ON-ből OD'-be ugyanakkora, de ellentétes irányú forgás visz át, mint ON-ból OM-be, vagyis OD' forgásszöge az ON alapiránytól mérve -α. Ezek szerint OD'-ből OB'-be 3α nagyságú forgás visz át.
Amíg α 0∘-tól 90∘-ig növekszik, a 3α forgásszög 0∘-tól 270∘-ig vesz fel minden értéket. A vizsgálandó β szög viszont nem lehet nagyobb 90∘-nál. Amíg 0∘≤α≤30∘, addig β egyenlő a 3α forgásszöggel. Amíg 30∘<α≤60∘, addig a forgásszög 90∘ és 180∘ közé esik, így β a kiegészítő szög, β=180∘-3α; ez α=60∘ esetén β=0∘-ot ad. (Valóban, α=60∘ esetén OB' és OD' egybeesnek, másrészt OU=OB/2=OA, tehát OAU egyenlő oldalú háromszög, ugyanígy OCV is, így AU és CV párhuzamosak, és párhuzamos egyenesek szögét szokás 0∘-nak tekinteni, mivel irányuk megegyező.)
α-t 60∘-on túl növelve 90∘-ig, β mértékszámát úgy kapjuk, hogy a 180∘ és 270∘ közé eső forgásszögből 180∘-ot kivonunk: β=3α-180∘. Ez még α=90∘ esetén is érvényes, hiszen akkor U=V=O, és így β=90∘. Ha viszont MO és ON egy egyenesbe esnek (α=0∘ vagy 180∘), akkor AU és CV is egy egyenesbe esik és így β=0∘.
II. Nem volna nehéz látni, hogy meggondolásaink kiterjeszthetők minden α-ra, de áttekinthetőbb képet kapunk, ha belátjuk, hogy egyrészt α-nak egymást 180∘-ra kiegészítő értékeihez, másrészt két egymástól 180∘-kal különböző α értékhez ugyanakkora β érték tartozik. Egyszerűbb az utóbbi belátása. Az OM egyenes önmagába megy át, ha egy tetszés szerinti helyzetből 180∘-kal elforgatjuk, így U és AU helyzete változatlan; C, D új helyzete, C*, ill. D* az előbbinek tükörképe O-ra, így ugyanez áll a V pont és a CV egyenes új V*, ill. C*V* helyzetére, ezért CV új helyzete párhuzamos a korábbival, így pedig az AU és CV egyenesek új helyzetei közti szögek egyenlők a korábbiakkal.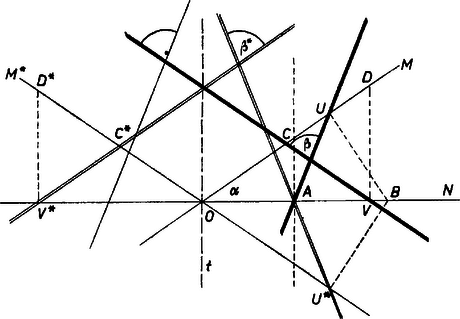
 
 
2. ábra
 

Legyen most α hegyesszög, α*=M*ON∢=180∘-α, a C, D, U, V pontoknak megfelelő pontok C*, D*, U*, V*. Ekkor OM*, C*, D* és V* az OM, C, D, V tükörképe az O-n átmenő, ON-re merőleges t egyenesre (2. ábra). Másrészt, mivel az OM* egyenes OM-ből ON-re való tükrözéssel is kapható, így U* az U tükörképe ON-re, s ezzel együtt AU* is AU tükörképe ON-re. Ekkor azonban AU és AU* az ON-re A-ban állított merőlegesre is tükrösek, ha pedig egy ezzel párhuzamos tengelyre (pl. t-re) tükrözzük AU*-t, AU-val párhuzamos egyenest kapunk. Így a β* szöget t-re tükrözve egyik szára CV-be megy át, a másik párhuzamos lesz AU-val, tehát a tükörkép egyállású β-val, s így β*=β; ezt akartuk belátni.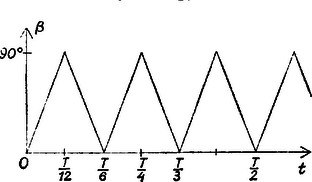
 
 
3. ábra
 

III. A β változásának grafikus ábrázolásához tudjuk, hogy OM az O körül állandó szögsebességgel forog, így α ‐ és vele β=3α is ‐ a t idővel arányos, a kérdéses szög nagyságát ábrázoló grafikon első, a körülfordulás első 12-ed részéhez tartozó szakasza egyenes. Ennélfogva a 2. és 3. szakaszban β=180∘-3α, ill. β=3α-180∘ értékét is egyenesszakasz ábrázolja. Jelöljük OM teljes körülfordulásának az idejét T-vel. A teljes grafikont ezek után úgy kapjuk, hogy a t=0-tól t=T/4-ig terjedő szakaszt a t=T/4 egyenesen tükrözzük, majd az így adódott ábrát T/2 szakasszal eltolva a (T/2, T) számköz fölött megismételjük (3. ábra).
 
 Major Péter (Budapest, Fazekas M. Gyak. Gimn., II. o. t.)