Kezdőlap


Feladat:	882. matematika gyakorlat	Korcsoport: 14-15	Nehézségi fok: átlagos
Megoldó(k):	Legányi András
Füzet:	1964/szeptember, 17 - 18. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Nevezetes egyenlőtlenségek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/december: 882. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. Mindegyik átló két háromszögre vágja szét a négyszöget. Ezekben a háromszög‐egyenlőtlenség alapján az 1. ábra jelöléseit használva

\begin{matrix} a + b > e, a + d > f, \\ c + d > e, b + c > f . \end{matrix}

Adjuk össze az ugyanazon átlót tartalmazó 2‐2 egyenlőtlenséget, majd szorozzuk az így adódó (nyilvánvalóan helyes) egyenlőtlenségeket a bennük szereplő átlóval Az átló pozitív, tehát a szorzások után is helyes egyenlőtlenségeket kapunk: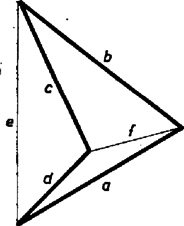

\begin{matrix} (a + b + c + d) e > 2 e^{2}, (a + b + c + d) f > 2 f^{2} . \end{matrix}

Az (1) állítás ezek összeadásával és kellő kiemelésekkel adódik.

1. ábra

Az állítás konkáv négyszögre is igaz, sőt hurkolt négyszögre is, az utóbbi esetben átlókon azokat a szakaszokat értve, melyeknek végpontjai a nem szomszédos

A

és

C

, ill.

B

és

D

csúcs-párok (2. ábra).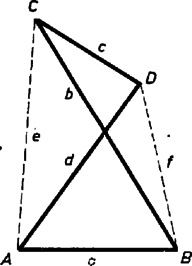

2. ábra

II. A PQRST ötszög 3‐3 egymás utáni csúcsával meghatározott háromszögeket 2‐2 szomszédos ötszögoldal és egy átló határolja. Ezért

\begin{matrix} p + q > p_{1}, q + r > q_{1}, r + s > r_{1}, & (3) \\ s + t > s_{1}, t + p > t_{1} . \end{matrix}

Avégett, hogy megkapjuk az átlók négyzetösszegét, szorozzuk meg a felírt egyenlőtlenségek mindkét oldalát a jobb oldalukon szereplő átlóval, majd adjuk össze az így kapott egyenlőtlenségeket:

\begin{matrix} p_{1} (p + q) + q_{1} (q + r) + r_{1} (r + s) + s_{1} (s + t) + \\ + t_{1} (t + p) > p_{1}^{2} + q_{1}^{2} + r_{1}^{2} + s_{1}^{2} + t_{1}^{2} . \end{matrix}

A végzett átalakításokkal mindig a bal oldalon kaptunk nagyobb számot, mert az átlók mértékszámai pozitívok. A bal oldalon kapott összeg azonos az állítás (2) kifejezésével, csupán alakban különböznek, itt ugyanis a bal oldal az átlók szerint van rendezve, (2) pedig az oldalak szerint. ‐ Ezzel az állításokat bebizonyítottuk.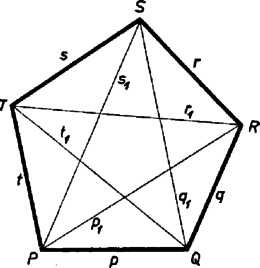

Legányi András (Tatabánya, Árpád g. I. o. t.)

3. ábra

Megjegyzés. Az ötszögre is kaphatunk az (1)-hez hasonló egyenlőtlenségeket, ha azt is felírjuk, hogy az 1‐1 csúcs elhagyásával adódó négyszögekben a 3 egymás utáni ötszögoldal összege nagyobb, mint a szabad végpontjaikat összekötő átló. Pl. az RSTP négyszögben

\begin{matrix} r + s + t > p_{1}, \end{matrix}

ezt (3) első egyenlőtlenségével összeadva kapjuk, hogy az ötszög (bármelyik) átlója kisebb a

k

kerület felénél:

\begin{matrix} k > 2 p_{1}, p_{1} < k / 2. \end{matrix}

Ezt mindegyik átlóra felírva kellő szorzás és összeadás után

\begin{matrix} k (p_{1} + q_{1} + r_{1} + s_{1} + t_{1}) > 2 (p_{1}^{2} + q_{1}^{2} + r_{1}^{2} + s_{1}^{2} + t_{1}^{2}) . \end{matrix}