| Feladat: | 881. matematika gyakorlat | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Arány P. , Babai László , Bárány I. , Bárdos Klára , Bódi Zoltán , Bóta K. , Deák J. , Domokos Zsuzsanna , Dömötör B. , Fodor Magdolna , Herényi István , Huhn A. , Karsai Kornélia , Király L. , Kiss Katalin , Körner János , Lippner Gy. , Lőrincz I. , Major P. (Bp. Bláthy) , Márki László , Mátrai Miklós , Nagy Klára , Siket Aranka , Simonovits András , Surányi László , Sükösd Cs. , Szabó M. , Szabó Zoltán , Szani E. , Szeidl László , Székely Gábor , Szemkeő Judit , Vesztergombi Katalin , Vicsek Tamás | ||
| Füzet: | 1964/október, 57 - 59. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Középpontos tükrözés, Középvonal, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1963/december: 881. matematika gyakorlat | ||
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.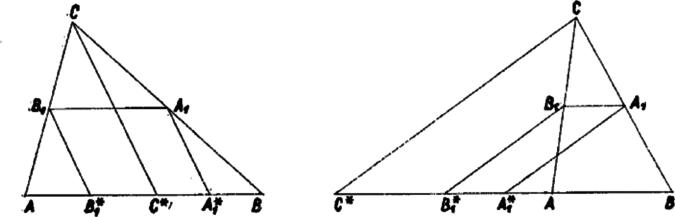 Vizsgáljuk az és a egyenesek metszéspontját. Az szakasz párhuzamos -vel, feleakkora és ellenkező irányú. Ez ismeretes, ha , , nincsenek egy egyenesen; az egyenesen levő pont esetén pedig válasszunk egy nem az egyenesen levő pontot, ahhoz rajzoljuk meg az és pontokat (1. ábra). Ekkor és mint középvonalak a , ill. háromszögbeli, egy irányban párhuzamosak -gal, így paralelogramma, tehát -gyel együtt is (ami az egyenesen van) fele akkora, mint , és azzal ellenkező irányú. Az szakasz -ből úgy keletkezik, hogy azt -ből mint külső hasonlósági pontból arányban kicsinyítjük, így is párhuzamos -vel, harmad akkora és egyező irányú vele. Ezek szerint és párhuzamosak és ellenkező irányúak. Ha és nincs egy egyenesen, akkor és az és egyenesek közti síksávban metszi egymást (2. ábra), metszéspontjukra , a hasonlóság aránya . Így az és a szakaszt egyaránt arányban osztja. 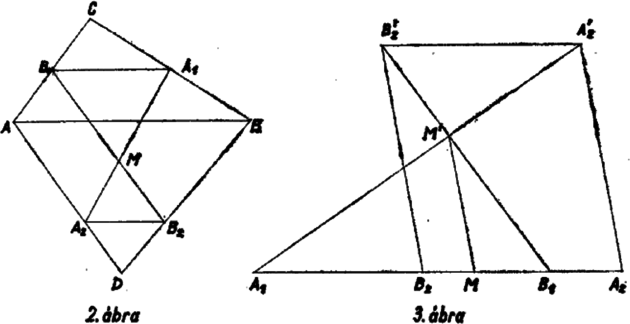 Ha az , , , pontok egy egyenesre esnek (3. ábra), akkor és metszéspontja határozatlan, de létezik egy egyértelműen meghatározott pont, amely mindkét szakaszt arányban osztja. Válasszunk ugyanis egy -vel párhuzamos, egyirányú és egyenlő szakaszt. Ekkor az előző meggondolás alapján belátható, hogy az és szakaszok metszéspontja mindkettőt arányban osztja. Messe az -n át -vel párhuzamosan húzott egyenes az egyenest -ben. Mivel , és , így az és szakaszt szintén arányban osztja. ‐ Világos, hogy ha és , vagy és egybeesik, akkor is egybeesik velük. Ha , , szerepét rendre , , -nek adjuk át, akkor meggondolásunk azt adja, hogy az és szakaszt arányban osztó pont egybeesik, így az pont az , , szakaszok mindegyikét arányban osztja, tehát egyeneseik közös pontja. Azt is nyertük, hogy az , , és az , , pontokból álló alakzatok hasonlósági pontja, az előbbi arányú kicsinyítéssel és -os elforgatással az utóbbiba megy át. Nem határozott pl. az egyenes, ha egybeesik -gyel; ez bekövetkezik, ha az szakasz -en túli meghosszabbításán van és . Ilyenkor és az egybeeső pontban metszik egymást, hiszen ezen át pl. -vel csak egy párhuzamos húzható, és azon miatt rajta van , és miatt rajta van . Előfordulhat, hogy a vizsgálandó három egyenes nem mind különböző, ha pl. , , nem mind különbözők, vagy ha , , , egy egyenes pontjai. Az ilyen esetek felsorolása felesleges, mert ilyenkor az állítás semmitmondó. Nem nehéz belátni, hogy -sel jelölve az háromszög súlypontját, és , így az és is hasonló helyzetű háromszögek, hasonlósági pontjuk szintén ; így , és (az és , ill. és , ill. és háromszögpárok hasonlósági pontjai) is egy egyenesen van. Az utolsó állítás akkor is igaz marad, ha , , tetszés szerinti hasonló helyzetű háromszögek; bizonyítása azonban sokkal nehezebb. |