Kezdőlap


Feladat:	872. matematika gyakorlat	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Béres László , Deák Jenő
Füzet:	1964/szeptember, 13 - 14. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Súlyvonal, Súlypont, Paralelogrammák, Gyakorlat
Hivatkozás(ok):	Feladatok: 1963/november: 872. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a $B M$ és $N D$ szakasz felezőpontja $K$ , ill. $L$ , és messe a $B D$ átlót az $A K$ , $A M$ , $A N$ , $A L$ egyenes rendre a $P$ , $Q$ , $B$ , $S$ pontban. A $P B K$ és a $P D A$ háromszögek hasonlók, ebből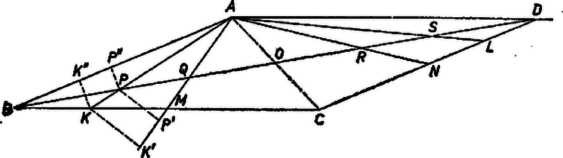

\begin{matrix} P B : P D = B K : D A = B K : B C = 1 : 4, \end{matrix}

így

B P

B D

átlónak 1/5 része.

Hasonlóan a

Q B M

és

Q D A

háromszögek hasonlóságából

\begin{matrix} Q B : Q D = B M : B C = 1 : 2, \end{matrix}

így

B Q = B D / 3

. Eszerint

P Q = B Q - B P = 2 B D / 15

. Ugyanígy látható, hogy

S D = B P = B D / 5

R S = P Q = 2 B D / 15

, végül

Q R = B D - B Q - R D = B D / 3

Deák Jenő (Budapest, Kölcsey F. g. II. o.t.)

II. megoldás. Húzzuk meg a paralelogramma

A C

átlóját és jelöljük a felezőpontját

O

-val. Ekkor az

A B C

háromszögben

A M

és

B O

súlyvonalak,

Q

a súlypont, ezért

B Q = 2 B O / 3 = B D / 3

. Hasonlóan

R D = B D / 3

, és így

Q R = B D / 3

.
Az

A P Q

és

A B P

háromszögek

A

-ból húzott magassága közös, ezért alapjaik

P Q : B P

aránya megegyezik területeik arányával. A területeket a közös

P

csúcsból húzott

P P'

, ill.

P P''

magassággal fogjuk kifejezni. Húzzunk még

K

-ból is

K K'

ill.

K K''

merőlegest

A Q

-ra, ill.

A B

-re. Ekkor a

P P' P''

és

K K' K''

háromszögek hasonlók, mert az előbbit

A

-ból úgy nagyítva, hogy

P

K

-ba,

P'

pedig

K'

-be kerüljön,

P''

A P''

és a

K

-ból

P P''

-vel párhozamosan húzott egyenes metszéspontjába kerül, ez pedig

K''

. Így

\begin{matrix} P P' : P P'' = K K' : K K'' . \end{matrix}

Ezt felhasználva a PQ:BP arány így alakítható át:

\begin{matrix} \frac{P Q}{B P} = \frac{A P Q}{A P B} = \frac{A Q \cdot P P'}{A B \cdot P P''} = \frac{A Q \cdot K K'}{A B \cdot K K''} = \frac{2}{3} \cdot \frac{A M \cdot K K'}{A B \cdot K K''} = \frac{2}{3} \cdot \frac{A M K}{A B K} = \frac{2}{3} \end{matrix}

(3 betű egymás után írásával a megfelelő háromszög területét jelöltük). Ismét felhasználtuk, hogy

Q

A B C

háromszög súlypontja, továbbá hogy az

A B K

és

A K M

háromszögek alapjai egyenlők, magasságuk közös. Eszerint

P Q = 2 B Q / 5 = 2 B D / 15

és

B P = 3 B Q / 5 = B D / 5

Béres László (Budapest, I. István g. III. o. t.)

Megjegyzés.

M

, ill.

K

helyett a

B C

oldal tetszés szerinti

X

pontját, továbbá az

A X

és

B D

egyenesek

Y

metszéspontját véve

B Y

-t a fenti eljárással kifejezhetjük

B D

-vel és a

B X : X C = λ

osztásaránnyal:

B Y = λ \cdot B D / (2 λ + 1)

. Az

M

pontra

λ = 1

K

-ra pedig

λ = 1 / 3

.
Ezen a módon a

B C

egyenes minden pontjához hozzárendelhető a

B D

egyenes egy pontja ‐ kivéve

C

-nek

B

-re vett tükörképét, és

B D

minden pontjához

B C

egy pontja, kivéve

D

-t. A

B C

és

B D

egyeneseken levő pontsorok között rokonság jött létre.¹

V. L.

¹Ezekről bővebben olvashat az érdeklődő a következő könyvben: Vigassy Lajos: Geometriai transzformációk (Tankönyvkiadó, Budapest, 1963)