Feladat: 848. matematika gyakorlat Korcsoport: 14-15 Nehézségi fok: átlagos
Megoldó(k):  Huhn Ágnes ,  Török László 
Füzet: 1964/március, 115 - 116. oldal  PDF  |  MathML 
Témakör(ök): Pont körüli forgatás, Magasságpont, Síkgeometriai számítások trigonometria nélkül háromszögekben, Síkbeli szimmetrikus alakzatok, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1963/május: 848. matematika gyakorlat

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az A, B, C csúcsból húzott magasság talppontja rendre D, F, K, a magasságpont M, az MA, MB, MC szakasz felezőpontja rendre H, L, E, végül az AB, AC szár felezőpontja J, ill. G. Be fogjuk látni, hogy ezek a DEFGHJKL sorrendben egy szabályos nyolcszög egymás utáni csúcsai. A nyolcszög szimmetrikus a háromszög AD tengelyére, más szóval a HD átlóra, ezért szabályos voltának bizonyításához elég megmutatni, hogy egyrészt DE, EF, FG és GH oldalai egyenlők, másrészt a D, E, F és G csúcsnál levő szögei, 135∘-o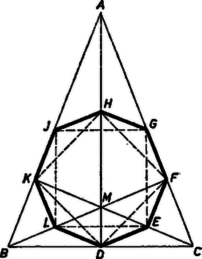sak.

 
 

A háromszög ACB szöge 67,5∘ és az AKC derékszögű háromszögből ACK∢=45∘, ezért KCB∢=ECD∢=22,5∘. CDM és CFM derékszögű háromszögek, ezért D és F a közös CM átfogó fölötti Thalész-kör pontjai. E kör középpontja E, tehát DE=EF=EC=EM; az ECD egyenlő szárú háromszögből egyrészt EDC∢=22,5∘, MDE∢=67,5∘, és így LDE∢=2⋅MDE∢=135∘, másrészt CED∢=135∘. A CEF egyenlő szárú háromszögből egyrészt CFE∢=45∘, és így EFG∢=135∘, másrészt CEF∢=90∘, ezért DEF∢=360∘-DEC∢-CEF∢=135∘.
GE az ACM háromszög középvonala, így párhuzamos AM-mel, ezért FGE∢=CAD∢=22,5∘, és így az EFG háromszögből FEG∢=22,5∘, ez a háromszög tehát egyenlő szárú, FG=FE.
GH ugyancsak középvonala az ACM háromszögnek, párhuzamos CM-mel. Ezért egyrészt AGH∢=ACK∢=45∘ és így FGH∢=135∘, másrészt EGHM paralelogramma, GH=EM=ED. A kitűzött egyenlőségek fennállását beláttuk, a bizonyítást befejeztük.
 
 Huhn Ágnes (Szeged, Tömörkény I. lg. I. o. t.)
 

II. megoldás. Bebizonyítjuk, hogy DFHK és EGJL egybevágó négyzetek, körülírt körük közös, és a kör középpontja körüli 45∘-os forgatással egymásba átvihetők. Ebből már következik, hogy DEFGHJKL körbeírt nyolcszög, és minden oldalához 45∘-os középponti szög tartozik, tehát a nyolcszög szabályos.
Az AFM és BFC derékszögű háromszögek egybevágók, mert oldalaik páronként merőlegesek, és így szögeik egyenlők, továbbá FM és FC befogóik egyenlők, mert FMC derékszögű, egyenlő szárú háromszög. A két háromszög F körüli 90∘-os forgatással egymásba megy át, eközben H és D, az átfogók felezőpontjai, egymásba mennek át, tehát FH=FD, és DFH∢=90∘. Eszerint DFH egyenlő szárú derékszögű háromszög, és a szimmetria miatt DFHK négyzet. Oldalának hossza DF=DC=BC/2, mert F a BC szakasz fölötti Thalész-körön van.
Az EGJL négyszög egymás utáni oldalai középvonalak az AMC, BCA, AMB, ill. BCM háromszögben, ezért rendre egyenlők az AM, BC, AM, BC szakasz felével, azaz egymással is, mert a fenti egybevágóság miatt AM=BC.
Másrészt rendre párhuzamosak a felsorolt szakaszokkal, tehát egymás utáni páronként merőlegesek egymásra, mert AM⊥BC. Így EGJL valóban négyzet.
Az EGJL négyzet köré írt kör átmegy F-en és K-n, mert F-ből a GL átmérő, K-ból az EJ átmérő derékszögben látszik. FK hossza a két négyzet egybevágósága miatt egyenlő a kör átmérőjével, így FK körünknek is átmérője, mert egy körben csak átellenes pontok vannak egymástól átmérőnyi távolságban. Így körünk a DFHK négyzetnek is körülírt köre. Végül a DH átló párhuzamos az EG oldallal, tehát a két négyzet egymáshoz képest valóban 45∘-kal van elfordulva.
 
 Török László (Pannonhalma, Benedek-rendi g. II. o. t.)